
【题目】如图,△ACB和△ECD中,∠ACB=∠ECD=a,且AC=BC,EC=DC,AE、BD交于P点,连CP
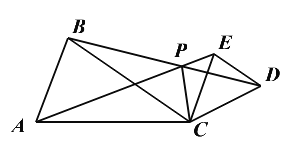
(1)求证:△ACE≌△BCD
(2)求∠APC的度数(用含a的式子表示)
【答案】(1)详见解析;(2)90°-![]() a.
a.
【解析】
(1)根据SAS即可证明结论;
(2)过C点分别作CH⊥AE,CG⊥BD,先利用全等的性质及三角形内角和证明∠BPA=∠ACB=a,再通过面积相等证明CH=CG,从而得到PC平分∠APD,然后利用角之间的关系即可得到结果.
解:(1)证明:∵∠ACB=∠DCE=a,
∴∠ACB+∠BCE=∠DCE+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中,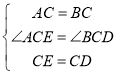 ,
,
∴△ACE≌△BCD(SAS);
(2)过C点分别作CH⊥AE于点H,CG⊥BD于点G,
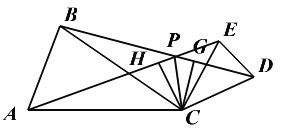
∵△ACE≌△BCD,
∴∠DBC=∠EAC,BD=AE,![]() ,
,
又∵∠BHP=∠AHC,
∴∠BPA=∠ACB=a,
∵![]() ,AE=BD,
,AE=BD,
∴CH=CG,
又∵CH⊥AE,CG⊥BD,
∴PC平分∠APD,
∴∠APC=![]() ∠APD=
∠APD=![]() (180°-∠BPA )=90°-
(180°-∠BPA )=90°-![]() a.
a.


科目:初中数学 来源: 题型:
【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔![]() 的高度,他从点
的高度,他从点![]() 处的观景塔出来走到点
处的观景塔出来走到点![]() 处.沿着斜坡
处.沿着斜坡![]() 从
从![]() 点走了
点走了![]() 米到达
米到达![]() 点,此时回望观景塔,更显气势宏伟.在
点,此时回望观景塔,更显气势宏伟.在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 且
且![]() ,再往前走到
,再往前走到![]() 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角![]() ,测得
,测得![]() 之间的水平距离
之间的水平距离![]() 米,则观景塔的高度
米,则观景塔的高度![]() 约为( ) 米. (
约为( ) 米. (![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
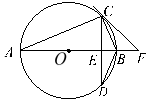
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将![]() 经过一次平移后得到
经过一次平移后得到![]() ,图中标出了点
,图中标出了点![]() 的对应点
的对应点![]() .(小正方形边长为1,
.(小正方形边长为1,![]() 的顶点均为小正方形的顶点)
的顶点均为小正方形的顶点)
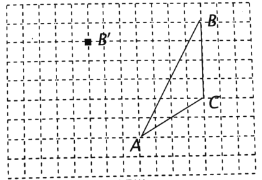
(1)补全![]() ;
;
(2)画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 中
中![]() 边上的高线
边上的高线![]() ;
;
(4)![]() 的面积为_____.
的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于给定的两点
中,对于给定的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,使得
,使得![]() 的面积等于1,即
的面积等于1,即![]() ,则称点
,则称点![]() 为线段
为线段![]() 的“单位面积点”.
的“单位面积点”.
解答下列问题:
如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
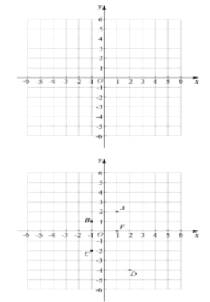
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,线段
中,线段![]() 的“单位面积点”是______.
的“单位面积点”是______.
(2)已知点![]() ,
,![]() ,点
,点![]() ,
,![]() 是线段
是线段![]() 的两个“单位面积点”,点
的两个“单位面积点”,点![]() 在
在![]() 的延长线上,若
的延长线上,若![]() ,直接写出点
,直接写出点![]() 纵坐标的取值范围.
纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣![]() ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 .
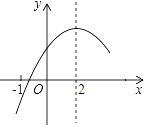
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少![]() .
.
A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格 | 1100 | 1400 |
销售价格 | 今年的销售价格 | 2000 |
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com