【题目】下列各比值中，是直角三角形的三边之比的是（ ）
A.
B.
C.
D.3:4:5
【答案】D
【解析】
利用勾股定理的逆定理：如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形．最长边所对的角为直角．由此判定即可．
解：A、设三边分别是x，2x，3x，∵x+2x=3x，∴三条线段不能组成三角形，不能组成直角三角形，故A选项错误；
B、设三边分别是2x，3x，4x，∵(2x)2+(3x)2≠(4x)2，∴三条线段不能组成直角三角形，故B选项错误；
C、设三边分别是3x，4x，6x，∵(3x)2+(4x)2≠(6x)2，∴三条线段不能组成直角三角形，故C选项错误；
D、设三边分别是3x，4x，5x，∵(3x)2+(4x)2=(5x)2，∴三条线段能组成直角三角形，故D选项正确；
故选：D．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】列出下列问题中的函数关系式，并判断它们是否为反比例函数．
（1）某农场的粮食总产量为1 500t，则该农场人数y（人）与平均每人占有粮食量x（t）的函数关系式；
（2）在加油站，加油机显示器上显示的某一种油的单价为每升4.75元，总价从0元开始随着加油量的变化而变化，则总价y（元）与加油量x（L）的函数关系式；
（3）小明完成100m赛跑时，时间t（s）与他跑步的平均速度v（m/s）之间的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD为∠CAF的角平分线，BD=CD，∠DBC=∠DCB，∠DCA=∠ABD，过D作DE⊥AC于E，DF⊥AB交BA的延长线于F，则下列结论：①△CDE≌△BDF；②CE=AB+AE；③∠BDC=∠BAC；④∠DAF=∠CBD.其中正确的结论有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ACB和△ECD中，∠ACB=∠ECD=a，且AC=BC，EC=DC,AE、BD交于P点，连CP
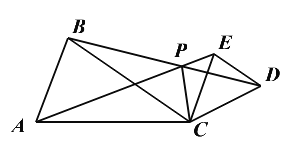
（1）求证:△ACE≌△BCD
（2）求∠APC的度数（用含a的式子表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了促进学生多样化发展，某校组织开展了社团活动，分别设置了体育类、艺术类、文学类及其它类社团（要求人人参与社团，每人只能选择一项）．为了解学生喜爱哪种社团活动，学校做了一次抽样调查．根据收集到的数据，绘制成如下两幅不完整的统计图， 请根据图中提供的信息，完成下列问题：
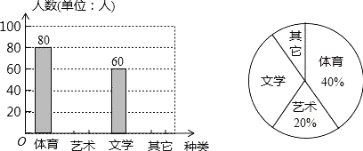
（1）此次共调查了 人；
（2）求文学社团在扇形统计图中所占圆心角为 度；
（3）请将条形统计图补充完整；
（4）若该校有 1500 名学生，请估计喜欢体育类社团的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
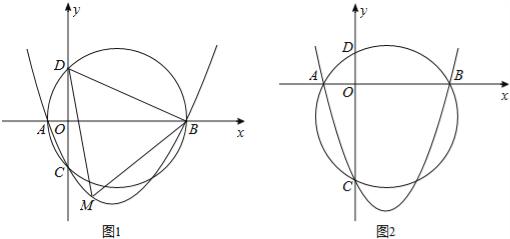
【题目】如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．
（1）如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；
①求此抛物线的表达式与点D的坐标；
②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；
（2）如图2，若a=1，求证：无论b，c取何值，点D均为定点，求出该定点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直角坐标系中的网格由单位正方形构成，
中，
点坐标为
，
点坐标为
，
点坐标为
．
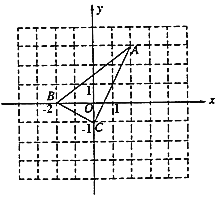
（1）
的长为_______；
（2）求证：
；
（3）若以、、及点
为顶点的四边形为平行四边形，写出点在第一象限时的坐标______．
查看答案和解析>>
科目：初中数学 来源： 题型：
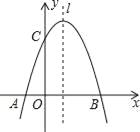
【题目】如图，已知抛物线y=
+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0），
（1）求m的值及抛物线的顶点坐标．
（2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观光塔是潍坊市区的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°．已知楼房高AB约是45m，根据以上观测数据可求观光塔的高CD是 m．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com