
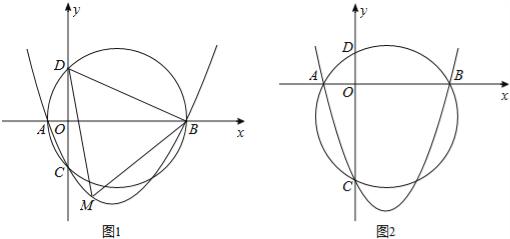
【题目】如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
【答案】(1)①![]() ,D(0,4);②36;(2)证明见解析,(0,1).
,D(0,4);②36;(2)证明见解析,(0,1).
【解析】试题分析:(1)①利用待定系数法求抛物线的解析式;利用勾股定理的逆定理证明∠ACB=90°,由圆周角定理得AB为圆的直径,再由垂径定理知点C、D关于AB对称,由此得出点D的坐标.
②求出△BDM面积的表达式,再利用二次函数的性质求出最值.
(2)根据抛物线与x轴的交点坐标、根与系数的关系、相似三角形求解.
试题解析:解:(1)①∵抛物线y=ax2+bx+c过点A(﹣2,0),B(8,0),
∴可设抛物线解析式为![]() .
.
∵抛物线y=ax2+bx+c过点C(0,﹣4),
∴![]() ,解得
,解得![]() .
.
∴抛物线的解析式为: ![]() ,即
,即![]() .
.
∵OA=2,OB=8,OC=4,∴AB=10.
如答图1,连接AC、BC.
由勾股定理得:AC=![]() ,BC=
,BC=![]() .
.
∵AC2+BC2=AB2=100,
∴∠ACB=90°.∴AB为圆的直径.
由垂径定理可知,点C、D关于直径AB对称,∴D(0,4).
②设直线BD的解析式为y=kx+b,
∵B(8,0),D(0,4),∴![]() ,解得
,解得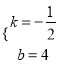 .∴直线BD解析式为:
.∴直线BD解析式为: ![]() .
.
设M(x, ![]() ),
),
如答图2,过点M作ME∥y轴,交BD于点E,则E(x, ![]() ).
).
∴ME=![]() .
.
∴S△BDM=S△MED+S△MEB=![]() ME(xE﹣xD)+
ME(xE﹣xD)+![]() ME(xB﹣xD)=
ME(xB﹣xD)=![]() ME(xB﹣xD)=4ME.
ME(xB﹣xD)=4ME.
∴S△BDM=![]()
∴当x=2时,△BDM的面积有最大值为36.
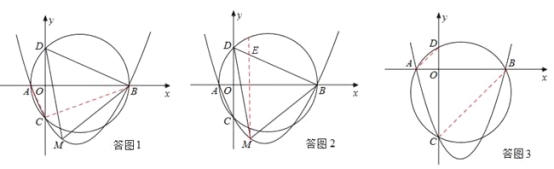
(2)证明:如答图3,连接AD、BC.
由圆周角定理得:∠ADO=∠CBO,∠DAO=∠BCO,
∴△AOD∽△COB.∴![]() .
.
设A(x1,0),B(x2,0),
∵已知抛物线y=x2+bx+c(c<0),∴OC=﹣c,x1x2=c.
∴![]() .∴
.∴![]() .
.
∴无论b,c取何值,点D均为定点,该定点坐标D(0,1).


科目:初中数学 来源: 题型:
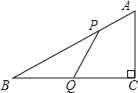
【题目】如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)若PQ⊥BC,求a的值;
(2)若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将![]() 经过一次平移后得到
经过一次平移后得到![]() ,图中标出了点
,图中标出了点![]() 的对应点
的对应点![]() .(小正方形边长为1,
.(小正方形边长为1,![]() 的顶点均为小正方形的顶点)
的顶点均为小正方形的顶点)
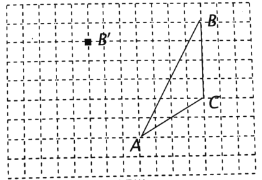
(1)补全![]() ;
;
(2)画出![]() 中
中![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 中
中![]() 边上的高线
边上的高线![]() ;
;
(4)![]() 的面积为_____.
的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于给定的两点
中,对于给定的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,使得
,使得![]() 的面积等于1,即
的面积等于1,即![]() ,则称点
,则称点![]() 为线段
为线段![]() 的“单位面积点”.
的“单位面积点”.
解答下列问题:
如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
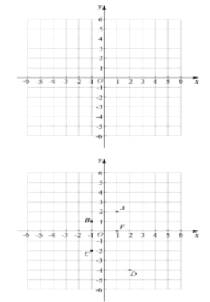
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,线段
中,线段![]() 的“单位面积点”是______.
的“单位面积点”是______.
(2)已知点![]() ,
,![]() ,点
,点![]() ,
,![]() 是线段
是线段![]() 的两个“单位面积点”,点
的两个“单位面积点”,点![]() 在
在![]() 的延长线上,若
的延长线上,若![]() ,直接写出点
,直接写出点![]() 纵坐标的取值范围.
纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
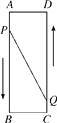
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到点B为止,点Q以2 cm/s的速度向点D移动,当点P停止运动时,点Q也停止运动.问:
(1)P,Q两点从开始出发多长时间时,四边形PBCQ的面积是33 cm2?
(2)P,Q两点从开始出发多长时间时,点P与点Q之间的距离是10 cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
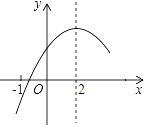
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣![]() ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 .
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
课题学习:如何解一元二次不等式?
例题:解一元二次不等式![]() .
.
解:![]()
![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有:
![]()
![]()
解不等式组![]() 得:
得:![]()
解不等式组![]() 得:
得:![]()
![]() 的解集为
的解集为![]() 或
或![]() .
.
即:一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
任务:(1)上面解一元二次不等式的过程中体现出了数学的一些基本思想方法,请在下列选项中选出你认为正确的一项:_____ ;(填选项即可)
A.分类讨论思想;B.数形结合思想;C.公理化思想;D.函数思想
(2)求一元二次不等式![]() 的解集为:_____ ;(直接填写结果,不写解答过程)
的解集为:_____ ;(直接填写结果,不写解答过程)
(3)仿照例题中的数学思想方法,求分式不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建立平面直角坐标系的网格纸中,每个小方格都是边长为1个单位长度的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0).
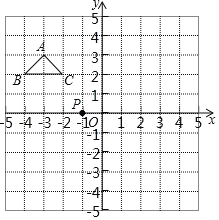
(1)把△ABC绕点P旋转180°得到△A’B’C’,作出△A’B’C’;
(2)把△ABC向右平移7个单位长度得到△A″B″C″,作出△A″B″C″;
(3)△A’B’C’与△A″B″C″是否成中心对称?若是,则找出对称中心P’,并写出其坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com