
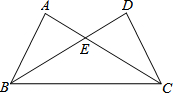
 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.分析 (1)根据AAS即可推出△ABE和△DCE全等;
(2)根据三角形全等得出EB=EC,推出∠EBC=∠ECB,根据三角形的外角性质得出∠AEB=2∠EBC,代入求出即可.
解答 (1)证明:在△ABE和△DCE中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠AEB=∠DEC}\\{AB=DC}\end{array}\right.$,
∴△ABE≌△DCE(AAS);
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
点评 本题考查了三角形外角性质和全等三角形的性质和判定的应用,主要考查学生的推理能力.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
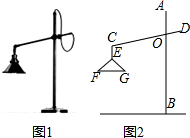 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
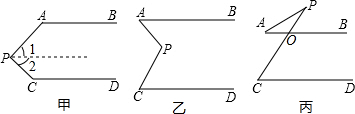 阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.
阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
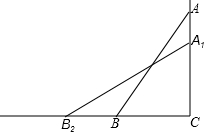 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
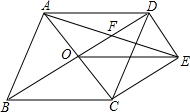 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com