Question

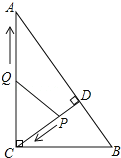
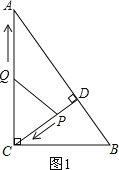
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；

（2）设△CPQ的面积为S，求S与t之间的函数关系式，并确定在运动过程中是否存在某一时刻t，使得S△CPQ：S△ABC=9：100？若存在，求出t的值；若不存在，则说明理由．

（3）是否存在某一时刻t，使得△CPQ为等腰三角形？若存在，求出所有满足条件的t的值；若不存在，则说明理由．

Answer 1

【答案】（1）线段CD的长为4.8；（2）当t=秒或t=3秒时，S△CPQ：S△ABC=9：100；（3）当t为2.4秒或秒或秒时，△CPQ为等腰三角形．

【解析】

试题分析：（1）利用勾股定理可求出AB长，再用等积法就可求出线段CD的长．

（2）过点P作PH⊥AC，垂足为H，通过三角形相似即可用t的代数式表示PH，从而可以求出S与t之间的函数关系式；利用S△CPQ：S△ABC=9：100建立t的方程，解方程即可解决问题．

（3）可分三种情况进行讨论：由CQ=CP可建立关于t的方程，从而求出t；由PQ=PC或QC=QP不能直接得到关于t的方程，可借助于等腰三角形的三线合一及三角形相似，即可建立关于t的方程，从而求出t．

解：（1）如图1，∵∠ACB=90°，AC=8，BC=6，

∴AB=10．

∵CD⊥AB，

∴S△ABC=BCAC=ABCD．

∴CD===4.8．

∴线段CD的长为4.8；

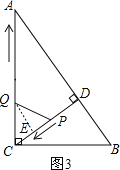
（2）①过点P作PH⊥AC，垂足为H，如图2所示．

由题可知DP=t，CQ=t．

则CP=4.8﹣t．

∵∠ACB=∠CDB=90°，

∴∠HCP=90°﹣∠DCB=∠B．

∵PH⊥AC，

∴∠CHP=90°．

∴∠CHP=∠ACB．

∴△CHP∽△BCA．

∴=．

∴=．

∴PH=﹣t．

∴S△CPQ=CQPH=t（﹣t）=﹣t2+t；

②存在某一时刻t，使得S△CPQ：S△ABC=9：100．

∵S△ABC=×6×8=24，且S△CPQ：S△ABC=9：100，

∴（﹣t2+t）：24=9：100．

整理得：5t2﹣24t+27=0．

即（5t﹣9）（t﹣3）=0．

解得：t=或t=3．

∵0≤t≤4.8，

∴当t=秒或t=3秒时，S△CPQ：S△ABC=9：100；

（3）存在

①若CQ=CP，如图1，

则t=4.8﹣t．

解得：t=2.4．…（7分）

②若PQ=PC，如图2所示．

∵PQ=PC，PH⊥QC，

∴QH=CH=QC=．

∵△CHP∽△BCA．

∴=．

∴=．

解得；t=．

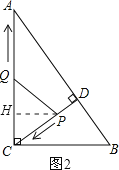
③若QC=QP，

过点Q作QE⊥CP，垂足为E，如图3所示．

同理可得：t=．

综上所述：当t为2.4秒或秒或秒时，△CPQ为等腰三角形．