
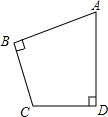
 如图,在四边形ABCD中,∠ABC=∠ADC=90°,
如图,在四边形ABCD中,∠ABC=∠ADC=90°,分析 (1)如图1,延长AB,DC交于E,由∠ABC=∠ADC=90°,∠BAC=60°,得到∠E=30°,∠EBC=90°,根据已知条件求得CE=2BC=4,BE=$\sqrt{3}$BC=2$\sqrt{3}$,然后根据三角形的面积即可得到结果;
(2)如图2,连接AC,由于S四边形ABCD=S△ABC+S△ADC=$\frac{1}{2}$BC•AB+$\frac{1}{2}$CD×AD=$\frac{1}{2}$BC•AB+$\frac{1}{2}$AD2=$\frac{1}{2}$BC•AB+$\frac{1}{2}$CD2根据AB+BC=8,求出BC2+AB2+2BC×AB=64,也是得到4S△ABC+4S△ACD=64,即可得到结论.
解答 解:(1)如图1,延长AB,DC交于E,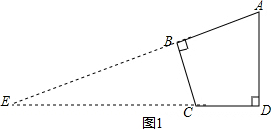
∵∠ABC=∠ADC=90°,∠BAC=60°,
∴∠E=30°,∠EBC=90°,
∵BC=CD=2,
∴CE=2BC=4,BE=$\sqrt{3}$BC=2$\sqrt{3}$,
∴AD=$\frac{\sqrt{3}}{3}$DE=$\frac{\sqrt{3}}{3}$(2+4)=2$\sqrt{3}$,
∴S四边形ABCD=S△AED-S△BCE=$\frac{1}{2}×$2$\sqrt{3}×$6-$\frac{1}{2}×$2×2$\sqrt{3}$=4$\sqrt{3}$;
(2)如图2,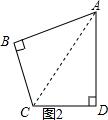 连接AC,
连接AC,
∵S四边形ABCD=S△ABC+S△ADC=$\frac{1}{2}$BC•AB+$\frac{1}{2}$CD×AD=$\frac{1}{2}$BC•AB+$\frac{1}{2}$AD2=$\frac{1}{2}$BC•AB+$\frac{1}{2}$CD2
∵AB+BC=8,
∴BC2+AB2+2BC×AB=64,
∴4S△ABC+4S△ACD=64,
∴S四边形ABCD=S△ABC+S△ADC=16.
点评 本题考查了四边形的面积,三角形的面积,等积变换,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
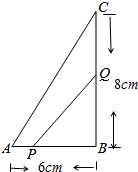 如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动.
如图,△ABC中,∠B=90°,点P从A点开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,当一方停止运动时另一方也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km
如图,某公路上有A、B、C三站,一辆汽车在上午8时从高A站5km的P地出发向C站匀速行驶,15min后离A站20km查看答案和解析>>
科目:初中数学 来源: 题型:解答题
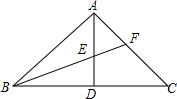 如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48-x=42-x | B. | 48-x=42+x | C. | 48-x=2(42+x) | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.4 | +1 | -0.5 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com