
 如图,△ABC的内切圆⊙O与三边分别相切于D、E、F三点,AB=7,BC=12,CA=11,
如图,△ABC的内切圆⊙O与三边分别相切于D、E、F三点,AB=7,BC=12,CA=11,分析 (1)设AF=x,根据切线长定理可得AE=AF=x,BF=BD=AB-AF=7-x,CE=CD=AC-AE=11-x,得方程:7-x+11-x=12,解此方程即可求得答案;
(2)作AM⊥BC于M,连接OA、OB、OC,OD、OE、OF,则∠AMB=∠AMC=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE=OF,由勾股定理求出AM,再由三角形面积的计算方法求出OD即可.
解答 解:(1)设AF=x,
∵△ABC的内切圆⊙O与三边分别相切于D、E、F三点,AB=7,BC=12,CA=11,
∴AE=AF=x,BF=BD=AB-AF=7-x,CE=CD=AC-AE=11-x,
∵BD+CD=BC,
∴7-x+11-x=12,
解得:x=3,
∴AF=3;
(2)作AM⊥BC于M,连接OA、OB、OC,OD、OE、OF,如图所示: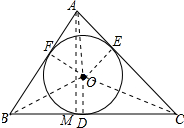
则∠AMB=∠AMC=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE=OF,
在Rt△ABM和Rt△ACM中,由勾股定理得:AM2=AB2-BM2=AC2-CM2,
设BM=x,则CM=12-x,
∴72-x2=112-(12-x)2,
解得:x=3,
∴BM=3,
∴AM=$\sqrt{{7}^{2}-{3}^{2}}$=2$\sqrt{10}$,
∵△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积=$\frac{1}{2}$BC•AM,
∴$\frac{1}{2}$(AB+BC+AC)OD═$\frac{1}{2}$BC•AM,
即$\frac{1}{2}$(7+12+11)×OD=$\frac{1}{2}$×12×2$\sqrt{10}$,
解得:OD=$\frac{4\sqrt{10}}{5}$,
即⊙O的半径为$\frac{4\sqrt{10}}{5}$.
点评 此题考查了三角形的内切圆、切线长定理、勾股定理、三角形面积的计算方法;熟练掌握切线长定理和勾股定理,由勾股定理和三角形的面积关系是⊙O的半径的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
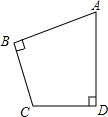 如图,在四边形ABCD中,∠ABC=∠ADC=90°,
如图,在四边形ABCD中,∠ABC=∠ADC=90°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
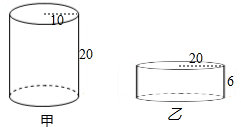 如图所示,有甲、乙两个容器,甲容器盛满了水,乙容器里没有水,现将甲容器中的水全部倒入乙容器,问:乙容器的水会不会溢出?如果不会溢出,请你求出倒入水后乙容器的水深;如果水会溢出,请你说明理由.(图中数据的单位:cm)
如图所示,有甲、乙两个容器,甲容器盛满了水,乙容器里没有水,现将甲容器中的水全部倒入乙容器,问:乙容器的水会不会溢出?如果不会溢出,请你求出倒入水后乙容器的水深;如果水会溢出,请你说明理由.(图中数据的单位:cm)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com