
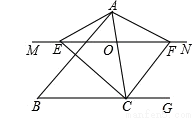
如图△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠GCA的平分线于点F.
(1)说明 EO=FO.
(2)当点O运动到何处,四边形AECF是矩形?说明你的结论.
(3)当点O运动到何处,AC与BC具有怎样的关系时,四边形AECF是正方形?为什么?
【解析】
(1)∵MN∥BC,
∴∠ECB=∠CEO,∠GCF=∠CFO,
∵CE,CF分别为∠BOC,∥GOC的角平分线,
∴∠ECB=∠ECO,∠GCF=∠OCF,
∴∠CEO=∠ECO,∠CFO=∠OCF,
∴OC=OE,OC=OF,
∴OE=OF,
(2)当O点运动到AC的中点时,四边形AECF为矩形,
理由:∵O点为AC的中点,
∴OA=OC,
∵OE=OF,OC=OE=OF,
∴OA=OC=OE=OF,
∴AC=EF,
∴四边形AECF是矩形,
(3)当O点运动到AC的中点时,AC⊥BC时,四边形AECF是正方形,
理由:∵O点为AC的中点时,四边形AECF是矩形,
∴AC=EF,
∵AC⊥BC,MN∥BC,
∴AC⊥EF,
∴四边形AECF是正方形.
【解析】
(1)由平行线的性质和角平分线的性质,推出∠ECB=∠CEO,∠GCF=∠CFO,∠ECB=∠ECO,∠GCF=∠OCF,通过等量代换即可推出∠CEO=∠ECO,∠CFO=∠OCF,便可确定OC=OE,OC=OF,可得OE=OF;
(2)当O点运动到AC的中点时,四边形AECF为矩形,根据矩形的判定定理(对角线相等且互相平分的四边形为矩形),结合(1)所推出的结论,即可推出OA=OC=OE=OF,求出AC=EF后,即可确定四边形AECF为矩形;
(3)当O点运动到AC的中点时,AC⊥BC时,四边形AECF是正方形,根据(2)所推出的结论,由AC⊥BC,MN∥BC,确定AC⊥EF,即可推出结论.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源:青岛版八年级下6.2平行四边形的判定 题型:解答题
在△ABC中,AB=AC,点P为△ABC所在平面内一点.
(1)当点P在BC边上,过点P分别作PD∥AC交AB于点D,PE∥AB交AC于点E,如图1.证明:AB=PD+PE;
(2)当点P在△ABC外部时,过点P分别作PD∥AC交AB于点D,PE∥AB交AC于点E,交BC于点F,请你在图2中画出相应的图形,并直接写出PD,PE,PF与AB满足的数量关系.(不必说明理由)

查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=5,则四边形CODE的周长是( )

A.5 B.7 C.9 D.10
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=AD,CB=CD时,四边形ABCD是菱形
C.当AB=AD=BC时,四边形ABCD是菱形
D.当AC=BD,AD=AB时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:填空题
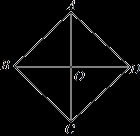
如图,在四边形ABCD中,AB=BC=CD=DA,对角线AC与BD相交于点O,若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是_______.
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:填空题
如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是______cm.

查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:选择题
如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
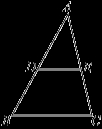
A.50° B.60° C.70° D.80°
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:解答题
如图,在△ABC中,CE平分∠ACB,AE⊥CE,延长AE交BC于点F,D是AB的中点,BC=20,AC=14,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com