
【题目】已知两个二次函数y1=x2+bx+c和y2=x2+m.对于函数y1 , 当x=2时,该函数取最小值.
(1)求b的值;
(2)若函数y1的图象与坐标轴只有2个不同的公共点,求这两个公共点间的距离;
(3)若函数y1、y2的图象都经过点(1,﹣2),过点(0,a﹣3)(a为实数)作x轴的平行线,与函数y1、y2的图象共有4个不同的交点,这4个交点的横坐标分别是x1、x2、x3、x4 , 且x1<x2<x3<x4 , 求x4﹣x3+x2﹣x1的最大值.
【答案】
(1)
解:由题意知:函数y1的对称轴为x=2,
∴﹣ ![]() =2,
=2,
∴b=﹣4
(2)
解:由题意知:△=b2﹣4c=16﹣4c,
当△>0时,
∴c<4,
此时函数y1与x轴有两个不同的交点,
由于若函数y1的图象与坐标轴只有2个不同的公共点,
∴c=0,
∴y1=x2﹣4x,
令y1=0,
∴x=0或x=4,
∴两个公共点间的距离为4,
当△=0时,
∴c=4,
此时抛物线与x轴只有一个交点,与y轴只有一个交点,
∴两个公共点间的距离,由勾股定理可求得: ![]() =2
=2 ![]()
(3)
解:∵函数y1、y2的图象都经过点(1,﹣2),
∴将(1,﹣2)代入函数y1和函数y2,
∴﹣2=1﹣4+c,
﹣2=1+m,
∴c=1,m=﹣3,
∴函数y1=x2﹣4x+1,函数y2=x2﹣3,
联立 ![]()
解得:x=1,y=﹣2,
∵过点(0,a﹣3)作x轴的平行线,与函数y1、y2的图象共有4个不同的交点,
∴﹣3<a﹣3<﹣2或a﹣3>﹣2
当﹣3<a﹣3<﹣2时,如图1,
即0<a<1,
令y=a﹣3代入y1,
∴x2﹣4x+4﹣a=0,
∴x3=2﹣ ![]() ,x4=2+
,x4=2+ ![]() ,
,
令y=a﹣3代入y2,
a﹣3=x2﹣3,
∴x1=﹣ ![]() ,x2=
,x2= ![]() ,
,
∴x4﹣x3+x2﹣x1=4 ![]() ,
,
∵0<a<1,
∴0<4 ![]() <4,
<4,
当a﹣3>﹣2,如图2,
即a>1,
令y=a﹣3代入y1,
∴x2﹣4x+4﹣a=0,
∴x2=2﹣ ![]() ,x4=2+
,x4=2+ ![]() ,
,
令y=a﹣3代入y2,
a﹣3=x2﹣3,
∴x1=﹣ ![]() ,x3=
,x3= ![]() ,
,
∴x4﹣x3+x2﹣x1=4,
综上所述,过点(0,a﹣3)(a为实数)作x轴的平行线,与函数y1、y2的图象共有4个不同的交点时,x4﹣x3+x2﹣x1的最大值为4.


【解析】(1)由于题意知x=2时,该函数取得最小值,所以x=2时该函数y1的对称轴;(2)若函数y1的图象与坐标轴只有2个不同的公共点,则分为两种情况讨论,一种是抛物线与x轴有两个交点时,另一种是抛物线与x轴有1个交点,然后分别求出C的值即可;(3)函数y1与y2经过(1,﹣2),所以可求出c与m的值,根据函数解析式画出图象可知,若过点(0,a﹣3)(a为实数)作x轴的平行线,与函数y1、y2的图象共有4个不同的交点时,则﹣3<a﹣3<﹣2或a﹣3>﹣2.
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a).


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),AB∥CD,探究∠BED与∠B+∠D的关系;
(2)如图(2),AB∥CD,类比上述方法,试探究∠E+∠G与∠B+∠F+∠D的关系,并写出推理过程;
(3)如图(3),AB∥CD,请直接写出你能得到的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作ABCD关于直线AD的对称图形AB1C1D 
(1)若m=3,试求四边形CC1B1B面积S的最大值;
(2)若点B1恰好落在y轴上,试求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE. 
(1)求证:AD∥BC;
(2)过点C作CG⊥AD于点F,交AE于点G,若AF=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF=cm. 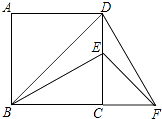
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是( ) 
A.![]() cm
cm
B.5cm
C.6cm
D.10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC. 
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com