Question

【题目】如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．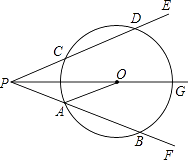
（1）求证：AP=AO；
（2）若tan∠OPB= ，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为 ， 能构成等腰梯形的四个点为或或 ．

Answer 1

【答案】
（1）证明：∵PG平分∠EPF，

∴∠DPO=∠BPO，

∵OA∥PE，

∴∠DPO=∠POA，

∴∠BPO=∠POA，

∴PA=OA

（2）解：过点O作OH⊥AB于点H，则AH=HB= AB，

∵tan∠OPB= ，∴PH=2OH，

设OH=x，则PH=2x，

由（1）可知PA=OA=10，∴AH=PH﹣PA=2x﹣10，

∵AH2+OH2=OA2，∴（2x﹣10）2+x2=102，

解得x1=0（不合题意，舍去），x2=8，

∴AH=6，∴AB=2AH=12

（3）P、A、O、C；A、B、D、C；P、A、O、D；P、C、O、B
【解析】（3）解：P、A、O、C；A、B、D、C或P、A、O、D或P、C、O、B． （1）由已知条件“射线PG平分∠EPF”求得∠DPO=∠BPO；然后根据平行线的性质，两直线OA∥PE，内错角∠DPO=∠POA；最后由等量代换知∠BPO=∠POA，从而根据等角对等边证明AP=AO；（2）设OH=x，则PH=2x．作辅助线OH（“过点O作OH⊥AB于点H”），根据垂径定理知AH=HB= AB；又由已知条件“tan∠OPB= ”求得PH=2OH；然后利用（1）的结果及勾股定理列出关于x的一元二次方程，解方程即可；（3）根据菱形的性质、等腰梯形的判定定理填空．