
 如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.求证:AM=DM.
如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.求证:AM=DM. 分析 连接AC,利用菱形的性质可得BD⊥AC,AB∥CD,然后证明四边形EFDB是平行四边形,可得DF=EB,再证明△AME≌△DMF可得AM=DM.
解答  证明:连接AC,
证明:连接AC,
∵四边形ABCD是菱形,
∴BD⊥AC,AB∥CD,
∵EF⊥AC,
∴EF∥BD,
∴四边形EFDB是平行四边形,
∴DF=EB,
∵E是AB中点,
∴AE=EB,
∴AE=DF,
∵AB∥CD,
∴∠EAM=∠ADF,
在△AEM和△DMF中$\left\{\begin{array}{l}{∠EAM=∠FDM}\\{∠AME=∠DMF}\\{AE=FD}\end{array}\right.$,
∴△AME≌△DMF(AAS),
∴AM=DM.
点评 此题主要考查了菱形的性质,关键是掌握菱形的对边平行,对角线互相垂直.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
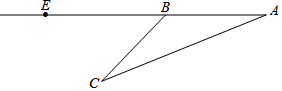 日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
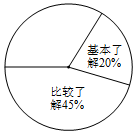 为纪念交通大学建校120周年进行宣传,附中中学某年级开展了主题为“交通大学历史知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了如图不完整的表格和扇形统计图.
为纪念交通大学建校120周年进行宣传,附中中学某年级开展了主题为“交通大学历史知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了如图不完整的表格和扇形统计图.| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
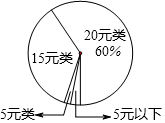 某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.| 类别 | 20元类 | 15元类 | 5元类 | 5元以下 |
| 各类合计捐款数 | 360 | m | 5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
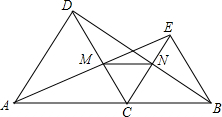 如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com