
����Ŀ����ͼ��ͼ1�ǡ�ABC��ͼ2�ǡ�8���Ρ������߶�AB��CD�ཻ�ڵ�O������AD��CB�γɵ�ͼ�Σ���ͼ3��һ���������״���Խ���������⣺
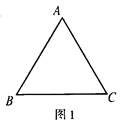

(1)ͼ1�ġ�ABC�У���A����B����C��_____����֤����д���Ľ��ۣ���Ҫ������֤�����̣�
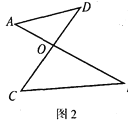
(2)ͼ2�ġ�8���Ρ��У���ֱ��д����A����B����C����D֮���������ϵ��_____��
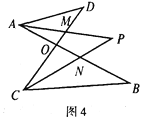
(3)����ͼ2�������£�����DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N(��ͼ4)����ֱ��д����P���D����B֮��������ϵ��____��
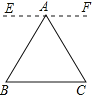
(4)ͼ3�еĵ�A�����Ƶ��߶�BE��ʱ����ֱ��д����CAD����B����C����D����E��____��
���𰸡� 180�� ��A+��D=��C+��B ��P=![]() ����D+��B�� 180��
����D+��B�� 180��
�������������������1���ȹ�A����EF��BC��������ֱ��ƽ�У��ڴ�����ȵó���B=��EAB����C=��CAF���ٸ��ݡ�EAB+��A+��CAF=180�㣬����֤����A+��B+��C�Ķ�����
��2�������������ڽǺͶ������ɵó���A+��D=��C+��B��
��3�����ݽ�ƽ���ߵ����ʵó���1=��2����3=��4���ٸ��ݶԶ��ǵ����ʣ��ó���1+��D=��3+��P����2+��P=��4+��B�����ɵó���D-��P=��P-��B���������������ɣ�
��4�����������ڽ�֮�͵��ں��������ڵ�һ����ǵó���CAD+��D=��CFG����B+��E=��CGF���ٸ����������ڽǺͶ��������ɵó��𰸣�
�����������1����A����EF��BC��
��EF��BC��
���B=��EAB����C=��CAF��
�ߡ�EAB+��A+��CAF=180�㣬
���A+��B+��C=180�㣻
��2���ߡ�A+��D+��AOD=��C+��B+��BOC=180�㣬
�֡ߡ�AOD=��BOC���Զ�����ȣ���
���A+��D=��C+��B��
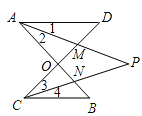
��3����AP��CP�ǡ�DAB����BCD��ƽ���ߣ�
���1=��2����3=��4��
�ߡ�1+��D=��3+��P����2+��P=��4+��B��
���D-��P=��P-��B��
���P=![]() ����D+��B����
����D+��B����
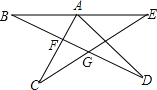
��4���ߡ�CAD+��D=��CFG����B+��E=��CGF��
�֡ߡ�C+��CFG+��CGF=180�㣬
���CAD+��B+��C+��D+��E=180�㣻



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
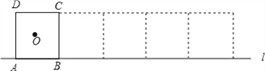
����Ŀ����ͼ�����߳�Ϊ1������Ϊ��O��������ABCD��ֱ��l�ϰ�˳ʱ�뷽������ÿ��ת��90����
��1����1���O������·�߳�Ϊ______����2���O������·�߳�Ϊ______����2013���O������·�߳�Ϊ______��
��2���ֱ������1�롢��2�롢��2013���A������·�߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
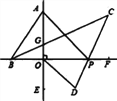
����Ŀ����ͼ��ֱ��AE��BF��O����һ�����ǰ�ABO��ͼ���ã���BAO=30��������ֱ�DZ���ֱ��BF��
AE�غϣ�PΪֱ��BF��һ���㣬BCƽ�֡�ABP��PCƽ�֡�APF��ODƽ�֡�POE��
��1�����BGO�Ķ�����
��2����ȷ����C���OAP֮���������ϵ����˵�����ɣ�
��3��P��ֱ�����˶�����C+��D��ֵ�Ƿ�仯���������仯��˵�����ɣ�����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
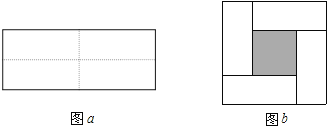
����Ŀ��ͼa��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼa�������ü����������ֳ��Ŀ�С�����Σ�Ȼ��ͼb����״ƴ��һ�������Σ�
��1���������ֲ�ͬ�ķ�����ͼb����Ӱ���ֵ������
����1�� ____ ��ֻ��ʽ��������
����2�� ______ ��ֻ��ʽ��������
��2���۲�ͼb��д������ʽ��m+n��2����m-n��2��mn֮��ĵ�����ϵ�� ______ ��
��3�����ݣ�2�����еĵ�����ϵ������������⣺��a+b=7��ab=5��
��a-b��2= ______ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У�����ȷ���� ( )
A.0�Ȳ���������Ҳ���Ǹ���B.0���෴����0
C.0����С����D.0�ľ���ֵ��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
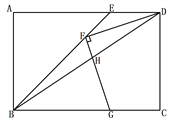
����Ŀ����ͼ������ABCD�У�BEƽ�֡�ABC��AD�ڵ�E��FΪBE��һ�㣬����DF����F��FG��DF��BC�ڵ�G������BD��FG�ڵ�H����FD = FG�� ![]() ��BG = 4����GH�ij�Ϊ__________��
��BG = 4����GH�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AC��BD������AB��ֱ��AC��BD���߶�AB��ƽ��ֳɢ١��ڡ��ۡ����ĸ����֣��涨�����ϸ��㲻�����κβ��֣�������P����ij������ʱ������PA��PB��������PAC����APB����PBD�����ǣ�����ʾ���й����˵�������غϵ���������ɵĽ���0��ǣ�

��1��������P���ڵڢٲ���ʱ����֤����APB=��PAC+��PBD��
��2��������P���ڵڢڲ���ʱ����APB=��PAC+��PBD�Ƿ��������ֱ�ӻش����������
��3��������P���ڵڢ۲���ʱ��ȫ��̽����PAC����APB����PBD֮��Ĺ�ϵ����д������P�ľ���λ�ú���Ӧ�Ľ��ۣ�ѡ������һ�ֽ��ۼ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ������ͼ��ʾ�ķ����������ϵĵ�C������OAB�У���OAB=90�㣬OA=2��AB=3���ҵ�O��A��C��ͬһ�����ϣ�OB=OC��
��1�������ϵĵ�C��ʾ�������� ����˵�������ϵĵ㲻�����Ա�ʾ�������������Ա�ʾ���������������ϵĵ���Ժ��� ��������һһ��Ӧ�Ĺ�ϵ��

��2������ͬѧ���������������������������ʾ��![]() �ĵ�D��
�ĵ�D��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
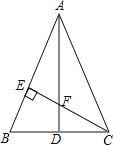
����Ŀ����ͼ����ABC�У�AB=AC����AD��BC��CE��AB������ֱ�ΪD��E��AD��CE�ཻ�ڵ�F������֪AE=CE.
(1)��֤����AEF�ա�CEB��
(2)��֤��AF=2CD
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com