
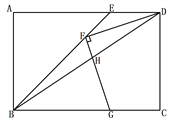
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD = FG, ![]() ,BG = 4,则GH的长为__________.
,BG = 4,则GH的长为__________.
【答案】![]()
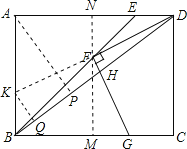
【解析】过点F作BC的垂线,分别交BC、AD于点M、N,则MN⊥AD,过点A作AP⊥BD于点P,延长DF交AB于点K,过点K作KQ⊥BD于点Q,如图所示。
∵FD⊥FG,
∴∠DFG=90°,
∴∠DFN+∠MFG=90°,
∵∠DNF=90°,
∴∠NDF+∠DFN=90°,
∴∠NDF=∠MFG,
在DNF和△FMG中,
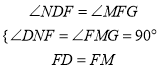 ,
,
∴△DNF≌△FMG(AAS),
∴DN=FM,NF=MG.
∵∠BAD=90°,BE平分∠ABC,
∴∠ABE=∠CBE=45°,
又∵FM⊥BM,
∴FM=BM,
∵BF=![]() ,
,
∴BM=FM=3,MG=BGBM=43=1,
∴NF=MG=1,AB=NM=4,AD=AN+ND=BM+FM=6,
∴BD=![]() .
.
由面积公式可知:S△ABD=![]() BDAP=
BDAP=![]() ABAD,即
ABAD,即![]() AP=4×6,
AP=4×6,
∴AP=![]() ,
,
∵NF∥AB,
∴△DNF∽△DAK,
∴![]() ,
,
∴AK=2NF=2,DK= ![]() =2
=2![]() ,DF=
,DF=![]() =
=![]() .
.
∴BK=ABAK=42=2,
∵KQ∥AP,
∴△BKQ∽△BAP,
∴![]() ,即,
,即, 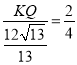 ,
,
∴KQ=![]() ,
,
∴BQ=![]() =
=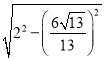 =
=![]() ,
,
∴DQ=BDBQ=![]()
![]() =
=![]() ,
,
∵∠DFH=∠DQK=90°,∠FDH=∠QDK,
∴△DFH∽△DQK,
∴![]() ,
,
即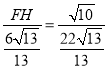 ,
,
∴FH=![]() ,
,
∴GH=FGFH=![]()
![]() =
=![]() .
.
故答案为: ![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,3为半径作圆.试判断:
①点C与⊙A的位置关系;②点B与⊙A的位置关系;③AB中的D点与⊙A的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句是命题的有( )
①两点之间线段最短;②不平行的两条直线有一个交点;③x 与 y 的和等于 0 吗?④对顶角不相等;⑤互补的两个角不相等;⑥作线段 AB.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
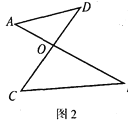
【题目】如图,图1是△ABC,图2是“8字形”(将线段AB、CD相交于点O,连接AD、CB形成的图形),图3是一个五角星形状,试解答下列问题:
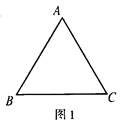

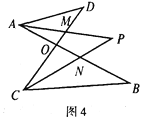
(1)图1的△ABC中,∠A+∠B+∠C=_____,并证明你写出的结论;(要有推理证明过程)
(2)图2的“8字形”中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_____;
(3)若在图2的条件下,作∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N(如图4).请直接写出∠P与∠D、∠B之间数量关系:____;
(4)图3中的点A向下移到线段BE上时,请直接写出∠CAD+∠B+∠C+∠D+∠E=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,林老师给出了下列方框中的一道题:
小聪和同桌小明讨论后,得出如下解答:
(![]() )特殊情况,探索结论
)特殊情况,探索结论
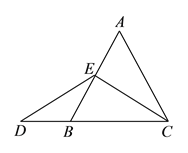
当点![]() 为
为![]() 的中点时,如图
的中点时,如图![]() ,确定线段
,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: ![]() ______
______ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
”或“![]() ”).
”).
(![]() )特例启发,解答问题
)特例启发,解答问题
解:题目中, ![]() 与
与![]() 的大小关系是
的大小关系是![]() __________
__________ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
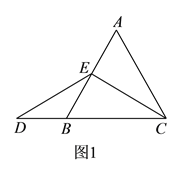
”或“![]() ”),理由如下:如图
”),理由如下:如图![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,(请你继续完成接下来的解题过程).
,(请你继续完成接下来的解题过程).
(![]() )拓展讨论,设计新题
)拓展讨论,设计新题
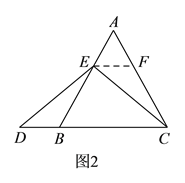
①互换林老师所给题的条件和结论,即:如图![]() 在等边三角形
在等边三角形![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,试确定线段
,试确定线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
②在等边三角形![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,若
,若![]() 的边长为
的边长为![]() ,
, ![]() ,求
,求![]() 的长为__________(请你直接写出结果).
的长为__________(请你直接写出结果).
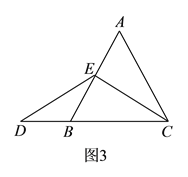
如图,在等边三角形![]() 中,点
中,点![]() 在
在![]()
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,
试确定线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:①∠DEF=∠DFE;②AE=AF;③DA平分∠EDF;④EF垂直平分AD.其中正确的序号是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() (3,0)、
(3,0)、![]() (-1,0).
(-1,0).
(1)求二次函数的解析式;
(2)如图,二次函数的图象与![]() 轴交于点
轴交于点![]() ,二次函数图象的对称轴与直线
,二次函数图象的对称轴与直线![]() 交于点
交于点![]() ,求
,求![]() 点的坐标;
点的坐标;
(3)在第一象限内的抛物线上有一点![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com