
ΓΨΧβΡΩΓΩ ΐ―ßΩΈ…œΘ§Ν÷άœ ΠΗχ≥ωΝΥœ¬Ν–ΖΫΩρ÷–ΒΡ“ΜΒάΧβΘΚ
–Γ¥œΚΆΆ§Ήά–ΓΟςΧ÷¬έΚσΘ§ΒΟ≥ω»γœ¬Ϋβ¥πΘΚ
Θ®![]() Θ©ΧΊ β«ιΩωΘ§ΧΫΥςΫα¬έ
Θ©ΧΊ β«ιΩωΘ§ΧΫΥςΫα¬έ
Β±Βψ![]() ΈΣ
ΈΣ![]() ΒΡ÷–Βψ ±Θ§»γΆΦ
ΒΡ÷–Βψ ±Θ§»γΆΦ![]() Θ§»ΖΕ®œΏΕΈ
Θ§»ΖΕ®œΏΕΈ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘ§«κΡψ÷±Ϋ”–¥≥ωΫα¬έΘΚ
ΒΡ¥σ–ΓΙΊœΒΘ§«κΡψ÷±Ϋ”–¥≥ωΫα¬έΘΚ ![]() ______
______ ![]() Θ®ΧνΓΑ
Θ®ΧνΓΑ![]() Γ±ΓΑ
Γ±ΓΑ ![]() Γ±ΜρΓΑ
Γ±ΜρΓΑ![]() Γ±Θ©Θ°
Γ±Θ©Θ°
Θ®![]() Θ©ΧΊάΐΤτΖΔΘ§Ϋβ¥πΈ Χβ
Θ©ΧΊάΐΤτΖΔΘ§Ϋβ¥πΈ Χβ
ΫβΘΚΧβΡΩ÷–Θ§ ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒ «
ΒΡ¥σ–ΓΙΊœΒ «![]() __________
__________ ![]() Θ®ΧνΓΑ
Θ®ΧνΓΑ![]() Γ±ΓΑ
Γ±ΓΑ ![]() Γ±ΜρΓΑ
Γ±ΜρΓΑ![]() Γ±Θ©Θ§άμ”…»γœ¬ΘΚ»γΆΦ
Γ±Θ©Θ§άμ”…»γœ¬ΘΚ»γΆΦ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Θ®«κΡψΦΧ–χΆξ≥…Ϋ”œ¬ά¥ΒΡΫβΧβΙΐ≥ΧΘ©Θ°
Θ§Θ®«κΡψΦΧ–χΆξ≥…Ϋ”œ¬ά¥ΒΡΫβΧβΙΐ≥ΧΘ©Θ°
Θ®![]() Θ©ΆΊ’ΙΧ÷¬έΘ§…ηΦΤ–¬Χβ
Θ©ΆΊ’ΙΧ÷¬έΘ§…ηΦΤ–¬Χβ
ΔΌΜΞΜΜΝ÷άœ ΠΥυΗχΧβΒΡΧθΦΰΚΆΫα¬έΘ§Φ¥ΘΚ»γΆΦ![]() ‘ΎΒ»±Ώ»ΐΫ«–Έ
‘ΎΒ»±Ώ»ΐΫ«–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œΘ§«“
ΒΡ―”≥ΛœΏ…œΘ§«“![]() Θ§ ‘»ΖΕ®œΏΕΈ
Θ§ ‘»ΖΕ®œΏΕΈ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΔΎ‘ΎΒ»±Ώ»ΐΫ«–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ§Βψ
…œΘ§Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ§«“
…œΘ§«“![]() Θ§»τ
Θ§»τ![]() ΒΡ±Ώ≥ΛΈΣ
ΒΡ±Ώ≥ΛΈΣ![]() Θ§
Θ§ ![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΈΣ__________Θ®«κΡψ÷±Ϋ”–¥≥ωΫαΙϊΘ©Θ°
ΒΡ≥ΛΈΣ__________Θ®«κΡψ÷±Ϋ”–¥≥ωΫαΙϊΘ©Θ°
»γΆΦΘ§‘ΎΒ»±Ώ»ΐΫ«–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() ‘Ύ
‘Ύ![]()
…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œΘ§«“
ΒΡ―”≥ΛœΏ…œΘ§«“![]() Θ§
Θ§
‘»ΖΕ®œΏΕΈ![]() ”κ
”κ![]() ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΒΡ¥σ–ΓΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®![]() Θ©
Θ©![]() ΘΜΘ®
ΘΜΘ®![]() Θ©
Θ©![]() Θ§ΦϊΫβΈωΘΜΘ®
Θ§ΦϊΫβΈωΘΜΘ®![]() Θ©ΔΌ
Θ©ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() Μρ
Μρ![]() Θ°
Θ°
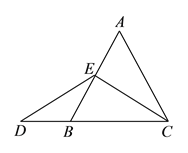
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§ΒψEΈΣABΒΡ÷–ΒψΘ§Φ¥Ω…ΒΟ≥ωCEΓΆABΘ§ΫχΕχΒΟ≥ωΓœECD=ΓœDΘ§Φ¥Ω…ΒΟ≥ωœΏΕΈED”κECΒΡ¥σ–ΓΙΊœΒΘΜ
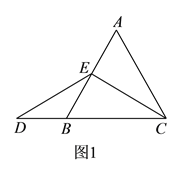
Θ®2Θ© Ήœ»ΒΟ≥ωBE=CFΘ§ΫχΕχάϊ”ΟΓςDBEΓ’ΓςEFCΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
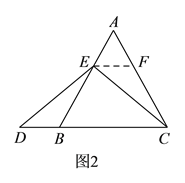
Θ®3Θ©ΔΌΉς![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ω…÷Σ
Θ§Ω…÷Σ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΫχΕχ÷ΛΟς
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΫχΕχ÷ΛΟς![]() Γ’
Γ’![]() Θ§Φ¥Ω…ΒΟ≥ω
Θ§Φ¥Ω…ΒΟ≥ω![]() ΘΜ
ΘΜ
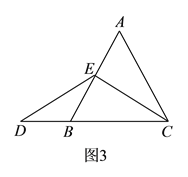
ΔΎΖ÷ΒψD‘ΎCBΒΡ―”≥ΛœΏ…œΓΔ‘ΎBCΒΡ―”≥ΛœΏ…œΝΫ÷÷«ιΩωΫχ––Χ÷¬έΦ¥Ω…ΒΟ.
‘ΧβΫβΈωΘΚΘ®![]() Θ©
Θ©![]() Θ°
Θ°
ΓΏ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ ![]() «
«![]() ÷–ΒψΘ§Γύ
÷–ΒψΘ§Γύ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ°
Θ°
ΓΏ![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ°
Θ°
Θ®![]() Θ©
Θ©![]()
‘ΎΒ»±Ώ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
Γύ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
Γύ![]() Θ§
Θ§
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Ά§άμ![]() Θ§
Θ§
”÷‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
‘Ύ![]() ΚΆ
ΚΆ![]() ÷–Θ§
÷–Θ§
 Θ§
Θ§
Γύ![]() Γ’
Γ’![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
Θ®![]() Θ©ΔΌΉς
Θ©ΔΌΉς![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§
‘ρΩ…÷Σ![]() ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
Γύ![]() Θ°
Θ°
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏ‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() ΚΆ
ΚΆ![]() ÷–Θ§
÷–Θ§
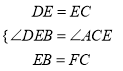 Θ§
Θ§
Γύ![]() Γ’
Γ’![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
ΔΎ![]() Θ§
Θ§
Γύ![]() Μρ
Μρ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ «“ΜΗω”Οά¥ Δ±§ΟΉΜ®ΒΡ‘≤ΉΕ–Έ÷Ϋ±≠,÷Ϋ±≠ΩΣΩΎΒΡ÷±ΨΕ EF ≥ΛΈΣ10cm,ΡΗœΏOE(OF)≥ΛΈΣ10cm,‘ΎΡΗœΏOF …œΒΡΒψA ¥Π”–“ΜΩ鱧Ϲ̮≤–‘ϋ«“FAΘΫ2cm,“Μ÷Μ¬λ“œ¥”±≠ΩΎΒΡΒψE ¥Π―Ί‘≤ΉΕ±μΟφ≈ά––ΒΫA Βψ,‘ρ¥Υ¬λ“œ≈ά––ΒΡΉνΕΧΨύάκΈΣ cmΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§(©¹3Θ§3)“ΜΕ®‘Ύ(ΓΓΓΓ)
A.ΒΎ“ΜœσœόB.ΒΎΕΰœσœόC.ΒΎ»ΐœσœόD.ΒΎΥΡœσœό
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ’ΐΖΫ–ΈΆχΗώ÷–Θ§ΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΨυΈΣ1ΗωΒΞΈΜ≥ΛΕ»Θ§ΓςABCΒΡ»ΐΗωΕΞΒψΒΡΈΜ÷Ο»γΆΦΥυ ΨΘ§œ÷ΫΪΓςABCΤΫ“ΤΘ§ ΙΒψA±δΜΜΈΣΒψAΓδΘ§ΒψBΓδΓΔCΓδΖ÷±π «BΓΔCΒΡΕ‘”ΠΒψΘ°

Θ®1Θ©«κΜ≠≥ωΤΫ“ΤΚσΒΡΓςAΓδBΓδCΓδΘ§≤Δ«σΓςAΓδBΓδCΓδΒΡΟφΜΐΘΜ
Θ®2Θ©»τΝ§Ϋ”AAΓδΘ§CCΓδΘ§‘ρ’βΝΫΧθœΏΕΈ÷°ΦδΒΡΙΊœΒ « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
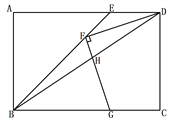
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§BEΤΫΖ÷ΓœABCΫΜAD”ΎΒψEΘ§FΈΣBE…œ“ΜΒψΘ§Ν§Ϋ”DFΘ§ΙΐFΉςFGΓΆDFΫΜBC”ΎΒψGΘ§Ν§Ϋ”BDΫΜFG”ΎΒψHΘ§»τFD = FGΘ§ ![]() Θ§BG = 4Θ§‘ρGHΒΡ≥ΛΈΣ__________Θ°
Θ§BG = 4Θ§‘ρGHΒΡ≥ΛΈΣ__________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉ““ΝΫΗωΆ§―ßΖ÷Ϋβ“ρ Ϋx2+ax+b ±Θ§ΦΉΩ¥¥μΝΥbΘ§Ζ÷ΫβΫαΙϊΈΣΘ®x+2Θ©Θ®x+4Θ©Θ§““Ω¥¥μΝΥaΘ§Ζ÷ΫβΫαΙϊΈΣΘ®x+1Θ©Θ®x+9Θ©Θ§‘ρ2a+bΘΫ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
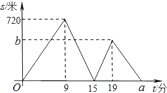
ΓΨΧβΡΩΓΩΦΉΓΔ““Εΰ»Υ¥”―ß–Θ≥ωΖΔ»ΞΩΤΦΦΙίΘ§ΦΉ≤Ϋ––“ΜΕΈ ±ΦδΚσΘ§““ΤοΉ‘––≥Β―ΊœύΆ§¬ΖœΏ––ΫχΘ§ΝΫ»ΥΨυ‘»ΥΌ«Α––Θ§ΥϊΟ«ΒΡ¬Ζ≥Χ≤νsΘ®ΟΉΘ©”κΦΉ≥ωΖΔ ±ΦδtΘ®Ζ÷Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΥυ ΨΘ°œ¬Ν–ΥΒΖ®ΘΚΔΌ““œ»ΒΫ¥οΩΤΦΦΙίΘΜΔΎ““ΒΡΥΌΕ» «ΦΉΥΌΕ»ΒΡ2.5±ΕΘΜΔέb=460ΘΜΔήa=25Θ°Τδ÷–’ΐ»ΖΒΡ «______Θ®Χν–ρΚ≈Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΓΔyΒΡΖΫ≥ΧΉι![]()
Θ®1Θ©«σΖΫ≥ΧΉιΒΡΫβΘ®”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ ΨΘ©ΘΜ
Θ®2Θ©»τΖΫ≥ΧΉιΒΡΫβ¬ζΉψΧθΦΰxΘΦ0Θ§«“yΘΦ0Θ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓœABDΚΆΓœBDCΒΡΤΫΖ÷œΏΫΜ”ΎEΘ§BEΫΜCD”ΎΒψFΘ§Γœ1+Γœ2=90ΓψΘ°

Θ®1Θ© ‘ΥΒΟςΘΚABΓΈCDΘΜ
Θ®2Θ©»τΓœ2=25ΓψΘ§«σΓœBFCΒΡΕ» ΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com