
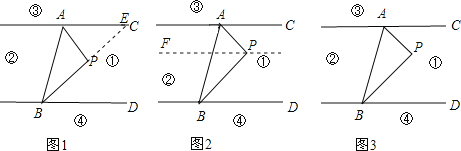
【题目】如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)

(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
【答案】(1)证明解解析(2)不成立(3)(a)当动点P在射线BA的右侧时,结论是:∠PBD=∠PAC+∠APB.(b)当动点P在射线BA上,结论是:∠PBD=∠PAC+∠APB.或∠PAC=∠PBD+∠APB或∠APB=0°,∠PAC=∠PBD(任写一个即可).(c)当动点P在射线BA的左侧时,结论是∠PAC=∠APB+∠PBD.选择(a)证明见解析
【解析】
试题分析:(1)如图1,延长BP交直线AC于点E,由AC∥BD,可知∠PEA=∠PBD.由∠APB=∠PAE+∠PEA,可知∠APB=∠PAC+∠PBD;
(2)过点P作AC的平行线,根据平行线的性质解答;
(3)根据P的不同位置,分三种情况讨论.
解:(1)解法一:如图1延长BP交直线AC于点E.
∵AC∥BD,∴∠PEA=∠PBD.
∵∠APB=∠PAE+∠PEA,
∴∠APB=∠PAC+∠PBD;
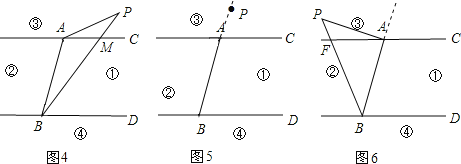
解法二:如图2
过点P作FP∥AC,
∴∠PAC=∠APF.
∵AC∥BD,∴FP∥BD.
∴∠FPB=∠PBD.
∴∠APB=∠APF+∠FPB
=∠PAC+∠PBD;
解法三:如图3,
∵AC∥BD,
∴∠CAB+∠ABD=180°,
∠PAC+∠PAB+∠PBA+∠PBD=180°.
又∠APB+∠PBA+∠PAB=180°,
∴∠APB=∠PAC+∠PBD.
(2)不成立.
(3)(a)当动点P在射线BA的右侧时,结论是:
∠PBD=∠PAC+∠APB.
(b)当动点P在射线BA上,结论是:
∠PBD=∠PAC+∠APB.
或∠PAC=∠PBD+∠APB或∠APB=0°,
∠PAC=∠PBD(任写一个即可).
(c)当动点P在射线BA的左侧时,
结论是∠PAC=∠APB+∠PBD.
选择(a)证明:
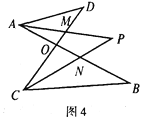
如图4,连接PA,连接PB交AC于M.
∵AC∥BD,
∴∠PMC=∠PBD.
又∵∠PMC=∠PAM+∠APM(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠PBD=∠PAC+∠APB.
选择(b)证明:如图5
∵点P在射线BA上,∴∠APB=0度.
∵AC∥BD,∴∠PBD=∠PAC.
∴∠PBD=∠PAC+∠APB
或∠PAC=∠PBD+∠APB
或∠APB=0°,∠PAC=∠PBD.
选择(c)证明:
如图6,连接PA,连接PB交AC于F
∵AC∥BD,∴∠PFA=∠PBD.
∵∠PAC=∠APF+∠PFA,
∴∠PAC=∠APB+∠PBD.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.

求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD ( )
∴∠B=_______( )
又∵∠B=∠D(已知 ),
∴∠D=_______( )
∴AD∥BE( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是△ABC,图2是“8字形”(将线段AB、CD相交于点O,连接AD、CB形成的图形),图3是一个五角星形状,试解答下列问题:
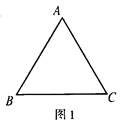

(1)图1的△ABC中,∠A+∠B+∠C=_____,并证明你写出的结论;(要有推理证明过程)
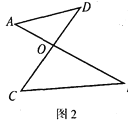
(2)图2的“8字形”中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_____;
(3)若在图2的条件下,作∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N(如图4).请直接写出∠P与∠D、∠B之间数量关系:____;
(4)图3中的点A向下移到线段BE上时,请直接写出∠CAD+∠B+∠C+∠D+∠E=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:①∠DEF=∠DFE;②AE=AF;③DA平分∠EDF;④EF垂直平分AD.其中正确的序号是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在检测一批刚出厂的足球的质量时,随机抽取了4个足球来测量其质量,把超过标准质量的克数记为正数,不足标准质量的克数记为负数,检测结果如下表:
足球的编号 | 1 | 2 | 3 | 4 |
与标准质量的差(克) | +3 | +2 | ﹣1 | ﹣2 |
则生产较合格的足球的编号是( )
A.1号B.2号C.3号D.4号
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有_____个白球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+m与y=-x+n的图象都经过点A(-2,0),且与y轴分别交于点B,C两点.
(1)在同一坐标系中,画出这两个函数的图象.
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com