练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下它的颜色后再放回口袋中，不断重复这一过程，共摸了100次球，发现有70次摸到红球．请你估计这个口袋中有_____个白球．

    【答案】3

    【解析】

    从一个总体得到一个包含大量数据的样本，我们很难从一个个数字中直接看出样本所包含的信息．这时，我们用频率分布直方图来表示相应样本的频率分布，从而去估计总体的分布情况．

    由题意可得，红球的概率为70%．则白球的概率为30%，

    这个口袋中白球的个数：10×30%＝3（个），

    故答案为：3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

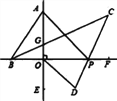
    【题目】如图，直线AE⊥BF于O，将一个三角板ABO如图放置（∠BAO=30°），两直角边与直线BF，

    AE重合，P为直线BF上一动点，BC平分∠ABP，PC平分∠APF，OD平分∠POE．

    （1）求∠BGO的度数；

    （2）试确定∠C与∠OAP之间的数量关系，并说明理由；

    （3）P在直线上运动，∠C+∠D的值是否变化？若发生变化，说明理由；若不变求其值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AC∥BD，连接AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA，PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）

    （1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；

    （2）当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（直接回答成立或不成立）

    （3）当动点P落在第③部分时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】同学甲用如图所示的方法作数轴上的点C：在△OAB中，∠OAB=90°，OA=2，AB=3，且点O、A、C在同一数轴上，OB=OC．

    （1）数轴上的点C表示的数是　 　，说明数轴上的点不仅可以表示有理数，还可以表示无理数，即数轴上的点可以和　 　数建立一一对应的关系．

    （2）仿照同学甲的作法，在下面的数轴上作出表示﹣的点D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE.

    （1）求证：△DEF是等腰三角形；

    （2）当∠A=50°时，求∠DEF的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

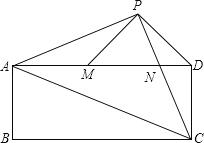
    【题目】已知：如图，在矩形ABCD中，AC是对角线．点P为矩形外一点且满足AP=PC，AP⊥PC．PC交AD于点N，连接DP，过点P作PM⊥PD交AD于M．

    （1）若AP=，AB=BC，求矩形ABCD的面积；

    （2）若CD=PM，求证：AC=AP+PN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

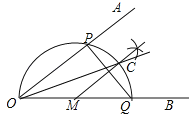
    【题目】已知∠AOB，作图．

    步骤1：在OB上任取一点M，以点M为圆心，MO长为半径画半圆，分别交OA、OB于点P、Q；

    步骤2：过点M作PQ的垂线交 于点C；

    步骤3：画射线OC．

    则下列判断：①=；②MC∥OA；③OP=PQ；④OC平分∠AOB，其中正确的个数为（　　）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

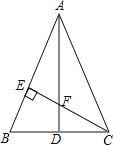
    【题目】如图，△ABC中，AB=AC，作AD⊥BC，CE⊥AB，垂足分别为D，E，AD和CE相交于点F，若已知AE=CE.

    (1)求证：△AEF≌△CEB；

    (2)求证：AF=2CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC．中，AB=BC，将△ABC绕点B顺时针旋转α度，得到△A1BC1，A1B交AC于点E，A1C1分别交AC、BC于点D、F，下列结论：①∠CDF=α，②A1E=CF，③DF=FC，④A1F=CE．其中正确的是　　（写出正确结论的序号）．

    查看答案和解析>>

    同步练习册答案