
【题目】已知![]() 和
和![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在射线
在射线![]() 上.
上.

(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC. .
【答案】(1)见解析;(2)见解析;
【解析】
(1)由∠BAC=∠EDF=60°,推出△ABC、△DEF为等边三角形,于是得到∠BCE+∠ACE=∠DCA+∠ECA=60°,推出△BCE≌△ACD(SAS),根据全等三角形的性质得到AD=BE,即可得到结论;
(2)在FA上截取FM=AE,连接DM,推出△AED≌△MFD(SAS),根据全等三角形的性质得到DA=DM=AB=AC,∠ADE=∠MDF,证得∠ADM=∠EDF=∠BAC,推出△ABC≌△DAM(SAS),根据全等三角形的性质得到AM=BC,即可得到结论.
证明:(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF为等边三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,
在△BCE和△ACD中
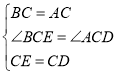
∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF;
(2)在FA上截取FM=AE,连接DM,
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
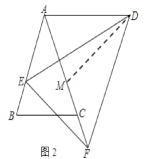
在△AED和△MFD中
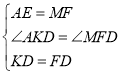 ,
,
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
在△ABC和△DAM中,
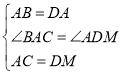 ,
,
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB于点O,若BC=8,AO=![]() ,求cos∠AED的值.
,求cos∠AED的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠α、∠β分别是与∠BAD、∠BCD相邻的补角,且∠B+∠CDA=140°,则∠α+∠β=( ).

A.260°B.150°C.135°D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com