
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
【答案】(1)![]() ;(2)
;(2)![]() ;(4)
;(4)![]() ,5,
,5,![]() ,
,![]() .
.
【解析】
试题(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4-2t,根据勾股定理列方程即可得到结论;
(2)当点P在∠CAB的平分线上时,如图1,过点P作PE⊥AB于点E,此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,根据勾股定理列方程即可得到结论;
(3)在Rt△ABC中,根据勾股定理得到AC=4cm,根据题意得:AP=2t,当P在AC上时,△BCP为等腰三角形,得到PC=BC,即4-2t=3,求得t=![]() ,当P在AB上时,△BCP为等腰三角形,若CP=PB,点P在BC的垂直平分线上,如图2,过P作PE⊥BC于E,求得t=
,当P在AB上时,△BCP为等腰三角形,若CP=PB,点P在BC的垂直平分线上,如图2,过P作PE⊥BC于E,求得t=![]() ,若PB=BC,即2t-3-4=3,解得t=5,③PC=BC,如图3,过C作CF⊥AB于F,由射影定理得;BC2=BFAB,列方程32=
,若PB=BC,即2t-3-4=3,解得t=5,③PC=BC,如图3,过C作CF⊥AB于F,由射影定理得;BC2=BFAB,列方程32=![]() ×5,即可得到结论.
×5,即可得到结论.
试题解析:(1)设存在点P,使得PA=PB,
此时PA=PB=2t,PC=4-2t,
在Rt△PCB中,PC2+CB2=PB2,
即:(4-2t)2+32=(2t)2,
解得:t=![]() ,
,
∴当t=![]() 时,PA=PB;
时,PA=PB;
(2)当点P在∠CAB的平分线上时,如图1,过点P作PE⊥AB于点E,
此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,
在Rt△BEP中,PE2+BE2=BP2,
即:(2t-4)2+12=(7-2t)2,
解得:t=![]() ,
,
∴当t=![]() 时,P在△ABC的角平分线上;
时,P在△ABC的角平分线上;
(3)在Rt△ABC中,∵AB=5cm,BC=3cm,
∴AC=4cm,
根据题意得:AP=2t,
当P在AC上时,△BCP为等腰三角形,
∴PC=BC,即4-2t=3,
∴t=![]() ,
,
当P在AB上时,△BCP为等腰三角形,
①CP=PB,点P在BC的垂直平分线上,
如图2,过P作PE⊥BC于E,
∴BE=![]() BC=
BC=![]() ,
,
∴PB=![]() AB,即2t-3-4=
AB,即2t-3-4=![]() ,解得:t=
,解得:t=![]() ,
,
②PB=BC,即2t-3-4=3,
解得:t=5,
③PC=BC,如图3,过C作CF⊥AB于F,
∴BF=![]() BP,
BP,
∵∠ACB=90°,
由射影定理得;BC2=BFAB,
即33=![]() ×5,
×5,
解得:t=![]() ,
,
∴当t=![]() ,5,
,5,![]() ,
,![]() 时,△BCP为等腰三角形.
时,△BCP为等腰三角形.


科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在射线
在射线![]() 上.
上.

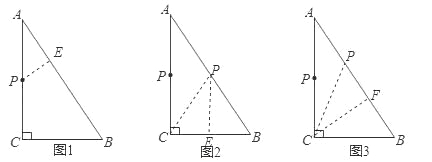
(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC. .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽查部分学生做了一次问卷调查,要求学生选出自己最喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
![]() 该调查的样本容量为______,
该调查的样本容量为______,![]() ______
______![]() ,“第一版”对应扇形的圆心角为______
,“第一版”对应扇形的圆心角为______![]() ;
;
![]() 请你补全条形统计图;
请你补全条形统计图;
![]() 若该校有1000名学生,请你估计全校学生中最喜欢“第三版”的人数.
若该校有1000名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,作斜边AB上中线CD,得到第1个三角形ACD;
,作斜边AB上中线CD,得到第1个三角形ACD;![]() 于点E,作
于点E,作![]() 斜边DB上中线EF,得到第2个三角形DEF;依次作下去
斜边DB上中线EF,得到第2个三角形DEF;依次作下去![]() 则第1个三角形的面积等于______,第n个三角形的面积等于______.
则第1个三角形的面积等于______,第n个三角形的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展课外社团活动,决定开设A:篮球,B:乒乓球,C:羽毛球,D:棋类四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.


(1)样本中最喜欢A项目的人数所占的百分比为________,其所在扇形统计图中对应的圆心角度数是________度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢乒乓球的学生人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
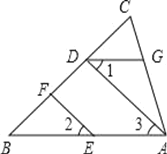
∵EF∥AD,(________)
∴∠2=______.(两直线平行,同位角相等;)
又∵∠1=∠2,(________)
∴∠1=∠3.(________)
∴AB∥DG.(________)
∴∠BAC+______=180°(________)
又∵∠BAC=70°,(________)
∴∠AGD=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速航行,到达位于灯塔B的北偏东l5°方向上的C处.

(1)求∠ACB的度数;
(2)求灯塔B到C处的距离.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com