
 如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{4}$x+1与x轴的正半轴相交于点A,B(点A位于点B的左侧),与y轴的正半轴交于点.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{4}$x+1与x轴的正半轴相交于点A,B(点A位于点B的左侧),与y轴的正半轴交于点.分析 (1)令x=0,求得y值,即可求出点C坐标,令y=0,解一元二次方程,求得x值,即可以求出点A、D坐标.
(2)首先假设存在,设出点P坐标,利用四边形面积求出点P的横纵坐标之间关系式,再利用△PBC等腰直角三角形性质,构造全等三角形,求出点P横纵坐标之间的关系式,联立两个关系式,即可以求出点P坐标.
解答 解:(1)令y=0,
得:$\frac{1}{4}$x2-$\frac{5}{4}$x+1=0,
即:x2-5x+4=0,
分解因式得:(x-1)(x-4)=0
得:x1=1,x2=5,
∴A(1,0),B(4,0).
令x=0,得y=1
∴C(0,1),
故答案为:A(1,0),B(4,0),C(0,1).
(2)存在.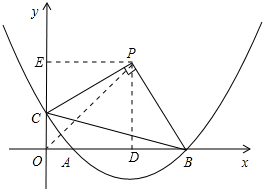
假设存在这样的点P,使得四边形PCOB的面积等于8,且△PBC是以点P为直角顶点的等腰直角三角形.
设点P的坐标为(x,y),连接OP.
则S四边形PCOB=S△PCO+S△POB
=$\frac{1}{2}$×1×x+$\frac{1}{2}$×4×y,
=$\frac{1}{2}$x+2y,
∴$\frac{1}{2}$x+2y=8,
∴x+4y=16
过P作PD⊥x轴,PE⊥y轴,垂足分别为D、E,
∴∠PEO=∠EOD=∠ODP=90°.
∴四边形PEOD是矩形
∴∠EPD=90°.
∴∠EPC=∠DPB.
∴△PEC≌△PDB,
∴PE=PD,即x=y.
由$\left\{\begin{array}{l}{x=y}\\{x+4y=16}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{16}{5}}\\{y=\frac{16}{5}}\end{array}\right.$,
∴点P($\frac{16}{5}$,$\frac{16}{5}$).
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).同时本题还考查二次函数与图形的综合利用,题目第一问比较简单,第二问较难,可以考查学生解决问题的综合能力.


科目:初中数学 来源: 题型:解答题
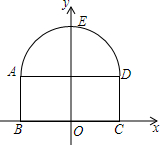 如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.
如图,在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com