
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;
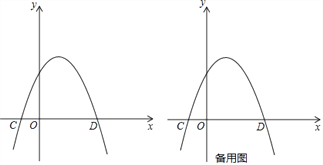
②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
【答案】(1)(-1,-4);y=x-3;(0,-3);(-1,-4);)(2)①m=-![]() ; ②m=-2
; ②m=-2
【解析】试题分析:(1)、由抛物线的顶点式可求得其顶点坐标,由伴随直线的定义可求得伴随直线的解析式,联立伴随直线和抛物线解析式可求得其交点坐标;(2)、①、可先用m表示出A、B、C、D的坐标,利用勾股定理可表示出AC2、AB2和BC2,在Rt△ABC中由勾股定理可得到关于m的方程,可求得m的值;②、由B、C的坐标可求得直线BC的解析式,过P作x轴的垂线交BC于点Q,则可用x表示出PQ的长,进一步表示出△PBC的面积,利用二次函数的性质可得到m的方程,可求得m的值.
试题解析:(1)、(-1,-4);y=x-3;(0,-3);(-1,-4)
(2)、①因为抛物线解析式为![]() ,所以其伴随直线为
,所以其伴随直线为![]() ,即
,即![]() 。
。
联立抛物线与伴随直线的解析式可得:![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,
,![]() ,
,
在![]() 中,令
中,令![]() 可计算出
可计算出![]() 或
或![]() ,所以
,所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() (抛物线开口向下,舍去),
(抛物线开口向下,舍去),![]() ,
,
所以当![]() 时,
时,![]() ;
;
②设直线![]() 的解析式为
的解析式为![]() ,如图过
,如图过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,如图所示:
,如图所示:
因为点![]() 的横坐标为
的横坐标为![]() ,所以
,所以![]() ,
,![]() ,因为
,因为![]() 是直线
是直线![]() 上方抛物线上的一个动点,
上方抛物线上的一个动点,
所以![]()
![]()
![]() ,
,
所以,![]() 。
。
当![]() 时,
时,![]() 的值有最大值
的值有最大值![]() ,所以
,所以![]() 取得最大值
取得最大值![]() 时,即
时,即![]() ,计算得出
,计算得出![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
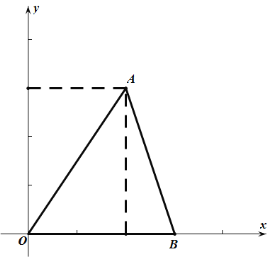
【题目】如图,平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n)其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
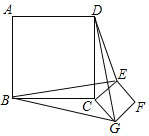
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2,其中正确结论是_____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
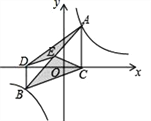
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
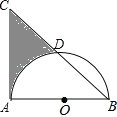
A. 16 B. 24-4π C. 32-4π D. 32-8π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知点P(m﹣1,n2),Q(m,n﹣1),其中m<0,则下列函数的图象可能同时经过P,Q两点的是( )
A.y=2x+bB.y=﹣x2+2x+c
C.y=ax+2 (a>0)D.y=ax2﹣2ax+c(a>0)
查看答案和解析>>
科目:初中数学 来源: 题型:
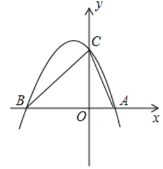
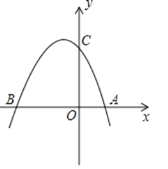
【题目】如图,抛物线y=﹣x2+mx+2与x轴交于点A,B,与y轴交于点C,点A的坐标为(1,0)
(1)求抛物线的解析式
(2)在抛物线的对称轴l上找一点P,使PA+PC的值最小,求出点P的坐标
(3)在第二象限内的抛物线上,是否存在点M,使△MBC的面积是△ABC面积的![]() ?若存在,求出点M的坐标,若不存在,请说明理由.
?若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com