
【题目】如图,抛物线y=﹣x2+mx+2与x轴交于点A,B,与y轴交于点C,点A的坐标为(1,0)
(1)求抛物线的解析式
(2)在抛物线的对称轴l上找一点P,使PA+PC的值最小,求出点P的坐标
(3)在第二象限内的抛物线上,是否存在点M,使△MBC的面积是△ABC面积的![]() ?若存在,求出点M的坐标,若不存在,请说明理由.
?若存在,求出点M的坐标,若不存在,请说明理由.
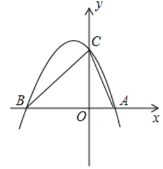
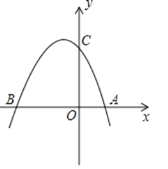
【答案】(1)y=﹣x2﹣x+2;(2)P(﹣![]() ,
,![]() );(3)存在,M(﹣1,2).
);(3)存在,M(﹣1,2).
【解析】
(1)把点A坐标代入抛物线的解析式求出m即可解决问题;
(2)如图1中,由A、B关于对称轴对称,连接BC交对称轴于P,连接PA,此时PA+PC的值最小.求出直线BC的解析式,即可解决问题;
(3)存在.如图,连接OM.设M(m,m2m+2).由S△MBC=![]() S△ABC,可得S△OBM+S△OCMS△ABC=
S△ABC,可得S△OBM+S△OCMS△ABC=![]() S△ABC,由此列出方程即可解决问题;
S△ABC,由此列出方程即可解决问题;
解:(1)∵y=﹣x2+mx+2经过点A(1,0),
∴0=﹣1+m+2,
∴m=﹣1,
∴抛物线的解析式为y=﹣x2﹣x+2.
(2)如图,由A、B关于对称轴对称,连接BC交对称轴于P,连接PA,此时PA+PC的值最小.
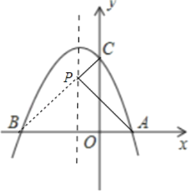
∵B(﹣2,0),C(0,2),设直线BC的解析式为y=kx+b,则有![]() ,
,
解得![]() ,
,
∴直线BC的解析式为y=x+2.
∵抛物线的对称轴x=﹣![]() ,
,
∴P(﹣![]() ,
,![]() ).
).
(3)存在.如图,连接OM.设M(m,﹣m2﹣m+2).
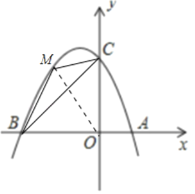
∵S△MBC=![]() S△ABC,
S△ABC,
∴S△OBM+S△OCM﹣S△ABC=![]() S△ABC,
S△ABC,
∴![]() ×2×(﹣m2﹣m+2)+
×2×(﹣m2﹣m+2)+![]() ×2×(﹣m)=
×2×(﹣m)=![]() ×
×![]() ×2×2,
×2×2,
解得m=﹣1,
∴M(﹣1,2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定:抛物线![]() 的伴随直线为
的伴随直线为![]() .例如:抛物线
.例如:抛物线![]() 的伴随直线为
的伴随直线为![]() ,即y=2x﹣1.
,即y=2x﹣1.
(1)在上面规定下,抛物线![]() 的顶点坐标为 ,伴随直线为 ,抛物线
的顶点坐标为 ,伴随直线为 ,抛物线![]() 与其伴随直线的交点坐标为 和 ;
与其伴随直线的交点坐标为 和 ;
(2)如图,顶点在第一象限的抛物线![]() 与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;
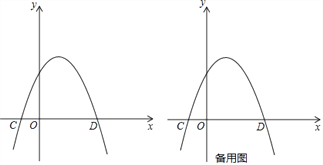
②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
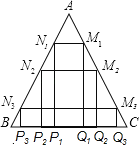
【题目】如图,在△ABC中,AB=AC=![]() ,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
A. 6B. ![]() C. 12D.
C. 12D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
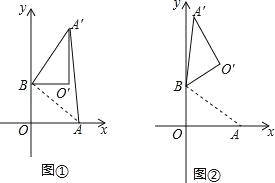
【题目】在平面直角坐标系中,O 为原点,点 A(4,0),点 B(0,3),把△ABO 绕点 B 逆时针旋转,得△A′BO′,点 A、O 旋转后的对应点为 A′、O′,记旋转角为ɑ.
(1)如图 1,若ɑ=90°,求 AA′的长;
(2)如图 2,若ɑ=120°,求点 O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,点E落在AD边上,若AF=4.AB=7.
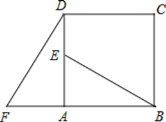
(1)旋转中心为 ;旋转角度为 ;
(2)求DE的长度;
(3)指出BE与DF的关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市面上贩售的防晒产品标有防晒指数![]() ,而其对抗紫外线的防护率算法为:防护率
,而其对抗紫外线的防护率算法为:防护率![]() ,其中
,其中![]() .
.
请回答下列问题:
(1)厂商宣称开发出防护率![]() 的产品,请问该产品的
的产品,请问该产品的![]() 应标示为多少?
应标示为多少?
(2)某防晒产品文宣内容如图所示.
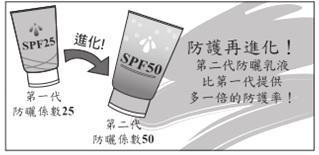
请根据![]() 与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
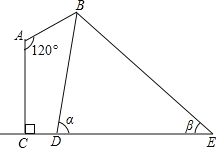
【题目】如图是某路灯在铅锤面内的示意图,灯柱AC的高为15.25米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为22米,从D、E两处测得路灯B的仰角分别为α和β,且tanα=8,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有三个完全相同的小球,分别标有数字2,3,4.从袋子中随机取出一个小球,用小球上的数字作为十位数字,然后放回,再取出一个小球,用小球上的数字作为个位数字,这样组成一个两位数,请用列表法或画树状图的方法完成下列问题.
(1)按这种方法组成两位数45是_____事件,填(“不可能”、“随机”、“必然”)
(2)组成的两位数能被3整除的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
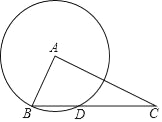
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com