
����Ŀ����һ�������Ĵ�����װ��������ȫ��ͬ��С�ֱ��������2��3��4.�Ӵ��������ȡ��һ��С����С���ϵ�������Ϊʮλ���֣�Ȼ��Żأ���ȡ��һ��С����С���ϵ�������Ϊ��λ���֣��������һ����λ���������б�������״ͼ�ķ��������������.
(1)�����ַ��������λ��45��_____�¼�����(�������������������������Ȼ��)
(2)��ɵ���λ���ܱ�3�����ĸ����Ƕ��٣�
���𰸡�(1)�����ܣ�(2)![]() .
.
��������
(1)�������⻭����״ͼ�ó����еȿ��ܵĽ����������ɵ���λ������������ٸ�������¼��ĸ���ɵó��𰸣�
(2)�����״ͼ��֪��ɵ���λ���ܱ�3����������33��42��24���ɸ��ʹ�ʽ������������.
�⣺(1)������ͼ���£�
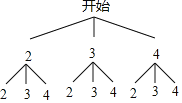
��ͼ��֪������ɵ���λ���У�22��23��24��32��33��34��42��43��44��
�����ַ��������λ��45�Dz������¼���
�ʴ�Ϊ�������ܣ�
(2)����״ͼ��֪��ɵ���λ���ܱ�3����������33��42��24��
����ɵ���λ���ܱ�3�����ĸ�����![]() ��
��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CD�ǡ�O���ң���CD��AB�ڵ�E��
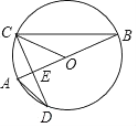
��1����֤����BCO����D��
��2����![]() ��AE��1�����ӻ�BD�ij���
��AE��1�����ӻ�BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��ax2+bx+3��a��0����x��ֱ���A����3��0����B���㣬��y�ύ�ڵ�C�������ߵĶ���E����1��4�����Գ��ύx���ڵ�F��
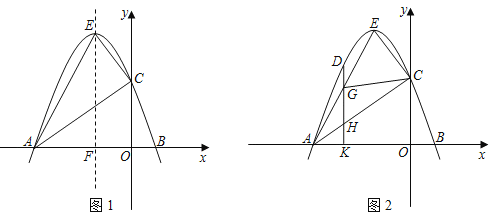
��1����ֱ��д�����������ߺ�ֱ��AE��ֱ��AC�Ľ���ʽ��
��2������AC��AE��CE���жϡ�ACE����״����˵�����ɣ�
��3����ͼ2����D����������һ���㣬���ĺ�����Ϊm���ҩ�3��m����1������D��DK��x���ڵ�K��DK�ֱ��߶�AE��AC�ڵ�G��H���ڵ�D���˶������У�
��DG��GH��HK�������߶��ܷ���ȣ�����ȣ��������D�����ꣻ������ȣ���˵�����ɣ�
���ڢٵ������£��ж�CG��AE��������ϵ����ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������y����![]() ������˵��������ǣ�������
������˵��������ǣ�������
A.ͼ���㣨1����3��
B.ͼ��ֲ��ڵ�һ��������
C.ͼ�����ԭ��Գ�
D.ͼ����������û�н���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB=AC=4��BC=6��D�ڵױ�BC�ϣ��ҡ�DAC=��ACD������ACD����AD����ֱ�߷��ۣ�ʹ�õ�C�䵽��E��������BE����ôBE�ij�Ϊ______.
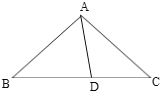
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90�㣬AC=3��BC=4���ֱ���AB��AC��BCΪ����AB��ͬ����������ABEF��ACPQ��BCMN���Ŀ���Ӱ���ֵ�����ֱ�ΪS1��S2��S3��S4����S1��S2+S3+S4���ڣ�������
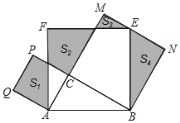
A. 4B. 6C. 8D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
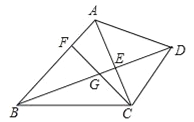
����Ŀ����֪����ͼ�����ı���ABCD�У�AB��CD���Խ���AC��BD���ڵ�E����F�ڱ�AB�ϣ�����CF���߶�BE�ڵ�G��CG2=GEGD��
��1����֤����ACF=��ABD��
��2������EF����֤��EFCG=EGCB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ķ���
������������α��е�����һ����Ŀ��
��ͼ1���ı���ABCD�������Σ�EΪBC����һ�㣬�ӳ�BA��F��ʹAF��CE������DE��DF������
����1����ECD�Ƶ�D˳ʱ����ת90��õ���FAD��
����2����ECD�ա�FAD��
����3����ת��ƽ�ơ���Գ���ͼ��ȫ�ȱ任�����ַ�ʽ��
����������
��1����ͼ2���ı���ABCD�������Σ�EΪBC����һ�㣬����DE������CDE��DE�۵�����C����G����EG��AB�ڵ�F������DF��
�ɵã���EDF���� ���㣻AF��FE��EC�����������ϵ���� ����
��2����ͼ3���ı���ABCD�����Ϊ8��AB��AD����DAB����BCD��90�㣬����AC����AC�ij��ȣ�
��3����ͼ4���ڡ�ABC�У���ACB��90�㣬CA��CB����D��E�ڱ�AB�ϣ���DCE��45�㣮д��AD��DE��EB���������ϵ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ�飺 ![]() ������������գ���ɱ���Ľⷨ��
������������գ���ɱ���Ľⷨ��
![]()
��1���ⲻ��ʽ��1������________��
��2���ⲻ��ʽ��2������________��
��3���Ѳ���ʽ ��1���� ��2���Ľ⼯�������ϱ�ʾ������
��4��ԭ����ʽ�Ľ⼯Ϊ________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com