
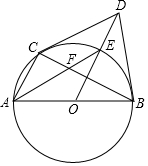
 如图,AB是⊙O的直径,BD与⊙O相切于B,C为⊙O上点,OD⊥BC,DO与⊙O相交于点E,AE交CB于F.
如图,AB是⊙O的直径,BD与⊙O相切于B,C为⊙O上点,OD⊥BC,DO与⊙O相交于点E,AE交CB于F.分析 (1)首先证明OD是线段BC的垂直平分线,推出DC=DB,推出∠DCB=∠DBC,由OC=OB,推出∠OCB=∠OBC,推出∠DCO=∠DCB+∠OCB=∠DBC+∠OBC=∠DBO,由DB是切线,推出OB⊥BD,推出∠DBO=90°,推出∠DCO=90°,即可解决问题.
(2)由△ACF∽△EHF,得$\frac{AC}{EH}$=$\frac{CF}{FH}$=$\frac{AF}{EF}$=3,设EH=a,则AC=3a,OH=$\frac{3}{2}$a,AB=5a,BC=4a,CH=BH=2a,FH=$\frac{1}{2}$a,CF=$\frac{3}{2}$a,在Rt△EFH中,根据EF2=FH2+EH2,列出方程即可解决问题.
解答 (1)证明:如图,连接OC,OD与BC交于点H.
∵OD⊥BC,
∴CH=HB,即OD垂直平分线段BC,
∴DC=DB,
∴∠DCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠DCO=∠DCB+∠OCB=∠DBC+∠OBC=∠DBO,
∵DB是切线,
∴OB⊥BD,
∴∠DBO=90°,
∴∠DCO=90°,
∴DC⊥OC,
∴CD是⊙O的切线.
(2)解:∵AB是直径,
∴∠ACB=90°,
∴∠OHB=∠ACB=90°,
∴OE∥AC,
∴△ACF∽△EHF,
∴$\frac{AC}{EH}$=$\frac{CF}{FH}$=$\frac{AF}{EF}$=3,设EH=a,则AC=3a,OH=$\frac{3}{2}$a,AB=5a,BC=4a,CH=BH=2a,FH=$\frac{1}{2}$a,CF=$\frac{3}{2}$a,
在Rt△EFH中,∵EF2=FH2+EH2,
∴1=$\frac{1}{4}$a2+a2,
∴a=$\frac{2\sqrt{5}}{5}$,
∴CF=$\frac{3\sqrt{5}}{5}$.
点评 本题考查切线的判定和性质、勾股定理、垂径定理、相似三角形的性质和判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
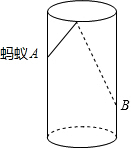 如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?
如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.
某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于A、B两点,以AB为腰长在第二象限内作等腰直角△ABC(其中∠CAB=90°).
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于A、B两点,以AB为腰长在第二象限内作等腰直角△ABC(其中∠CAB=90°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com