练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

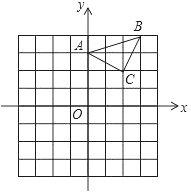
    【题目】已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．（正方形网格中，每个小正方形的边长是1个单位长度）．

    （1）作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1，并直接写出C1点的坐标；

    （2）作出△ABC关于原点O成中心对称的△A2B2C2，并直接写出B2的坐标．

    【答案】（1）图见解析，C1（﹣1，1）；（2））图见解析，B2（﹣3，﹣4）．

    【解析】

    （1）利用旋转的性质得出对应点位置进而得出答案；

    （2）利用关于原点对称点的性质得出对应点位置进而得出答案．

    解：（1）如图所示：△A1B1C1，即为所求，C1（﹣1，1）；

    （2）如图所示：△A2B2C2，即为所求，B2（﹣3，﹣4）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

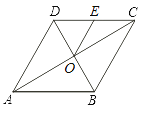
    【题目】如图，菱形ABCD的对角线AC、BD相交于点O，点E为边CD的中点，若菱形ABCD的周长为16，∠BAD＝60°,则△OCE的面积是（ ）

    A. B. 2 C. D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，菱形ABCD的顶点A(3，0)，顶点B在y轴正半轴上，顶点D在x轴负半轴上，若抛物线y=－x2－5x+c经过点B、C，则菱形ABCD的面积为（ ）

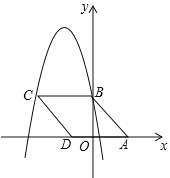
    A.15B.20C.25D.30

    查看答案和解析>>

    科目：初中数学 来源： 题型：

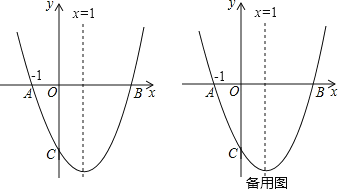
    【题目】如图，二次函数y＝x2+bx+c的图象与x轴交于A，B两点，与y轴交于点C，且关于直线x＝1对称，点A的坐标为（﹣1，0）．

    （1）求二次函数的表达式；

    （2）连接BC，若点P在y轴上时，BP和BC的夹角为15°，求线段CP的长度；

    （3）当a≤x≤a+1时，二次函数y＝x2+bx+c的最小值为2a，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

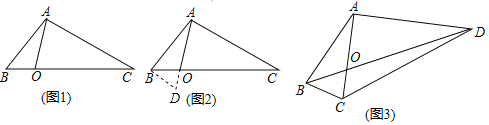
    【题目】（1）某学校“智慧方园”数学社团遇到这样一个题目：

    如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=，BO：CO=1：3，求AB的长．

    经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．

    请回答：∠ADB=　 　°，AB=　 　．

    （2）请参考以上解决思路，解决问题：

    如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】取什么值时，关于的方程有两个相等的实数根？求出这时方程的根.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知点A（1，2）和点B（4，5），当直线y＝kx﹣2k（k为常数）与线段AB有交点时，k的取值范围为（　　）

    A.k≤﹣2或k≥B.﹣2≤k≤

    C.﹣2≤k≤0或0≤k≤D.﹣2＜k＜0或0＜k＜

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明和小刚一起做游戏，游戏规则如下：将分别标有数字 1， 2， 3， 4 的 4 个小球放入一个不透明的袋子中，这些球除数字外都相同．从中随机摸出一个球记下数字后放回，再从中随机摸出一个球记下数字．若两次数字差的绝对值小于 2，则小明获胜，否则小刚获胜．这个游戏对两人公平吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，函数的图象与函数（）的图象相交于点，并与轴交于点．点是线段上一点，与的面积比为2：3．

    （1） ， ；

    （2）求点的坐标；

    （3）若将绕点顺时针旋转，得到，其中的对应点是，的对应点是，当点落在轴正半轴上，判断点是否落在函数（）的图象上，并说明理由．

    查看答案和解析>>

    同步练习册答案