
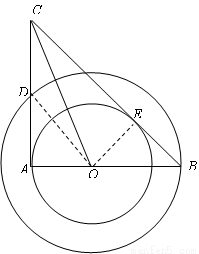
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.

(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积.(结果保留 )
)
(1)BC所在直线与小圆相切.理由见解析;(2)AC+AD=BC.理由见解析;(3)16πcm2.
【解析】
试题分析:(1)只要证明OE垂直BC即可得出BC是小圆的切线,即与小圆的关系是相切.
(2)利用全等三角形的判定得出Rt△OAD≌Rt△OEB,从而得出EB=AD,从而得到三者的关系是前两者的和等于第三者.
(3)根据大圆的面积减去小圆的面积即可得到圆环的面积.
试题解析:(1)BC所在直线与小圆相切.
理由如下:
过圆心O作OE⊥BC,垂足为E;
∵AC是小圆的切线,AB经过圆心O,
∴OA⊥AC;
又∵CO平分∠ACB,OE⊥BC,
∴OE=OA,
∴BC所在直线是小圆的切线.
(2)AC+AD=BC.
理由如下:
连接OD.
∵AC切小圆O于点A,BC切小圆O于点E,
∴CE=CA;
∵在Rt△OAD与Rt△OEB中,
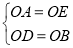 ,
,
∴Rt△OAD≌Rt△OEB(HL),
∴EB=AD;
∵BC=CE+EB,
∴BC=AC+AD.
(3)∵∠BAC=90°,AB=8cm,BC=10cm,
∴AC=6cm;
∵BC=AC+AD,
∴AD=BC-AC=4cm,
∵圆环的面积为:S=π(OD)2-π(OA)2=π(OD2-OA2),
又∵OD2-OA2=AD2,
∴S=42π=16π(cm2).
考点:1.切线的判定与性质;2.全等三角形的判定与性质;3.勾股定理.


科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区八年级上学期期中测试数学试卷(解析版) 题型:选择题
下列图形中,是轴对称图形的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区九年级上学期期中测试数学试卷(解析版) 题型:选择题
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )

A.3:2 B.3:1 C.1:1 D.1:2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宝应县九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB、CD的上方,求AB和CD间的距离.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宝应县九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,△ABC内接于⊙O,CB=a,CA=b,∠A-∠B=90°,则⊙O的半径为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].

(1)如图①,对△ABC作变换[60°, ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,BC=1,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com