Question

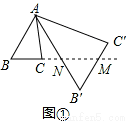
将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．

（1）如图①，对△ABC作变换[60°，]得△AB′C′，则S△AB′C′：S△ABC= ；直线BC与直线B′C′所夹的锐角为 度；

（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，BC=1,对△ABC 作变换[θ，n]得△AB'C'，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；

（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB'C'为平行四边形，求θ和n的值．

 

Answer 1

（1） 3:1，60；（2）60,2; （3） ．

【解析】

试题分析：（1）由旋转与相似的性质，即可得S△AB′C′：S△ABC=3，然后由△ABN与△B′MN中，∠B=∠B′，∠ANB=∠B′NM，可得∠BMB′=∠BAB′，即可求得直线BC与直线B′C′所夹的锐角的度数；

（2）由四边形 ABB′C′是矩形，可得∠BAC′=90°，然后由θ=∠CAC′=∠BAC′-∠BAC，即可求得θ的度数，又由含30°角的直角三角形的性质，即可求得n的值；

（3）由四边形ABB′C′是平行四边形，易求得θ=∠CAC′=∠ACB=72°，又由△ABC∽△B′BA，根据相似三角形的对应边成比例，易得AB2=CB•BB′=CB（BC+CB′），继而求得答案．

试题解析：（1）根据题意得：△ABC∽△AB′C′，

∴S△AB′C′：S△ABC=（A′B′:AB）2=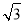（）2=3，∠B=∠B′，

∵∠ANB=∠B′NM，

∴∠BMB′=∠BAB′=60°；

（2）∵四边形 ABB′C′是矩形，

∴∠BAC′=90°．

∴θ=∠CAC′=∠BAC′-∠BAC=90-30=60．

在 Rt△ABB′中，∠ABB'=90°，∠BAB′=60°，

∴∠AB′B=30°，

∴n=.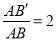

（3）∵四边形ABB′C′是平行四边形，

∴AC′∥BB′，

又∵∠BAC=36°，

∴θ=∠CAC′=∠AC′B′=72．

∴∠BB′A=∠BAC=36°，而∠B=∠B，

∴△ABC∽△B′BA，

∴AB：BB′=CB：AB，

∴AB2=CB•BB′=CB（BC+CB′），

而CB′=AC=AB=B′C′，BC=1，

∴AB2=1（1+AB），

∴AB=，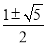

∵AB＞0，

∴n=．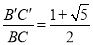

考点：1..相似三角形的判定与性质；2.平行四边形的性质；3.矩形的性质；4.旋转的性质．