
【题目】如图,已知正方形ABCD边长为6,将其折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是( )

A.15 B.12 C.8 D.6
【答案】B
【解析】
试题分析:根据翻折的性质可得DF=EF,设EF=x,表示出AF,然后利用勾股定理列方程求出x,从而得到AF、EF的长,再求出△AEF和△BGE相似,根据相似三角形对应边成比例列式求出BG、EG,然后根据三角形周长的定义列式计算即可得解.
解:由翻折的性质得,DF=EF,设EF=x,则AF=6﹣x.
∵点E是AB的中点,
∴AE=BE=![]() ×6=3.
×6=3.
在Rt△AEF中,AE2+AF2=EF2,即32+(6﹣x)2=x2.
解得x=![]() .
.
∴AF=6﹣![]() =
=![]() .
.
∵∠FEG=∠D=90°,
∴∠AEF+∠BEG=90°.
∵∠AEF+∠AFE=90°,
∴∠AFE=∠BEG.
又∵∠A=∠B=90°,
∴△AEF∽△BGE.
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() .
.
解得:BG=4,EG=5.
∴△EBG的周长=3+4+5=12.
故选:B.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
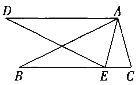
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能说明命题“关于x的一元二次方程x2+mx+4=0,当m<﹣2时必有实数解”是假命题的一个反例为( )
A. m=﹣4 B. m=﹣3 C. m=﹣2 D. m=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为4a2■ab+9b2,你认为这个二项整式应是( )
A. 2a+3b B. 2a﹣3b C. 2a±3b D. 4a±9b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月,生物学家发现一种病毒的长度约为0.0000043米,利用科学记数法表示为( )
A. 4.3×106米 B. 4.3×10﹣5米 C. 4.3×10﹣6米 D. 43×107米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com