
【题目】圆的内接等腰三角形ABC,圆的半径为10,如果底边BC的长为16,那么△ABC的面积为
科目:初中数学 来源: 题型:
【题目】学校为了奖励初三优秀毕业生,计划购买一批平板电脑和一批学习机,经投标,购买1台平板电脑3 000元,购买1台学习机800元.
(1)学校根据实际情况,决定购买平板电脑和学习机共100台,要求购买的总费用不超过168 000元,则购买平板电脑最多多少台?
(2)在(1)的条件下,购买学习机的台数不超过平板电脑台数的1.7倍.请问有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上一点,∠COE是直角,OF平分∠AOE.
(1)如图①,若∠COF=34°,则∠BOE=________;若∠COF=n°,则∠BOE=________;∠BOE与∠COF的数量关系为________________.
(2)当射线OE绕点O逆时针旋转到如图②的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
(3)在图③中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=2AB,取AC中点D;
(2)在(1)的条件下,如果AB=4,求线段BD的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ABC=90°,AB=BC=![]() ,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .
,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里,据预测,海鲜的市场价格将每天每千克上涨1元.冷冻存放这批海鲜每天需要支出各种费用合计310元,而且这些海鲜在冷库中最多存放160天,同时平均每天有3千克的海鲜变质.
(1)设x天后每千克该海鲜的市场价格为y元,试写出y与x之间的函数关系式;
(2)若存放x天后,将这批海鲜一次性出售.设这批海鲜的销售总额为P元,试写出P与x之间的函数关系式;
(3)小李将这批海鲜存放多少天后出售可获得最大利润,最大利润是多少元?(利润W=销售总额﹣收购成本﹣各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足![]()
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
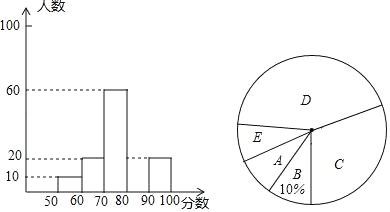
【题目】2018“体彩杯”重庆开州汉丰湖半程马拉松赛开跑前一周,某校七年级数学研究学习小组在某十字路口随机调查部分市民对“半马拉松赛”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
A | 50<n≤60 |
B | 60<n≤70 |
C | 70<n≤80 |
D | 80<n≤90 |
E | 90<n≤100 |
(1)本次调查的总人数为 人,在扇形统计图中“C”所在扇形的圆心角的度数为 度;
(2)补全频数分布图;
(3)若在这一周里,该路口共有7000人通过,请估计得分超过80的大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com