
【题目】如图1,已知△ABC中,AB=AC,点D是△ABC外一点(与点A分别在直线BC两侧),且DB=DC,过点D作DE∥AC,交射线AB于E,连接AE交BC于F.
(1)求证:AD垂直BC;
(2)如图1,点E在线段AB上且不与B重合时,求证:DE=AE;
(3)如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE的数量关系.
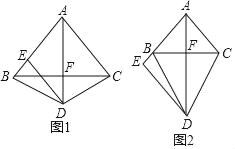
【答案】(1)见解析;(2)见解析;(3)DE=AC+BE.
【解析】
(1)根据线段垂直平分线的判定定理得到直线AD是BC的垂直平分线,证明结论;
(2)证明△ABD≌△ACD,得到∠BAD=∠CAD,根据平行线的性质得到∠BAD=∠CAD,等量代换得到∠BAD=∠EDA,根据等腰三角形的判定定理证明;
(3)仿照(2)的证明方法解答.
(1)∵AB=AC,DB=DC,
∴直线AD是BC的垂直平分线,
∴AD垂直BC;
(2)在△ABD和△ACD中,
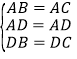 ,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠EDA=∠CAD,
∴∠BAD=∠EDA,
∴DE=AE;
(3)DE=AC+BE.
由(2)得,∠BAD=∠CAD,
∵DE∥AC,
∴∠EDA=∠CAD,
∴∠BAD=∠EDA,
∴DE=AE,
∵AB=AC,
∴DE=AB+BE=AC+BE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)当t为何值时,△DEF为直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)请写出图1、图2、图3分别能解释的乘法公式.


(2)用4个全等的长和宽分别为![]() 、
、![]() 的长方形拼摆成一个如图4的正方形,请你写出这三个代数式
的长方形拼摆成一个如图4的正方形,请你写出这三个代数式![]() 、
、![]() 、
、![]() 之间的等量关系.
之间的等量关系.
(3)根据(2)中你探索发现的结论,完成下列问题:
①当![]() ,
,![]() 时, 则
时, 则![]() 的值为 .
的值为 .
②设![]() ,
,![]() ,计算:
,计算:![]() 的结果.
的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.
 (保留作图痕迹,不要求写作法和证明);
(保留作图痕迹,不要求写作法和证明);
(2)在(1)条件下,连结BD,当BC=3cm,AB=5cm时,求△BCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(-3,-6)的抛物线![]() 经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程
经过点(-1,-4),下列结论:①b2>4ac;②ax2+bx+c≥-6;③若点(-2,m),(-5,n)在抛物线上,则m>n;④关于x的一元二次方程![]() 的两根为﹣5和﹣1,其中正确的有( )
的两根为﹣5和﹣1,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(45°)是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D)在同一条直线上).请求出旗杆MN的高度.(参考数据:![]() ,
,![]() ,结果保留整数)
,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,可以单独用正三角形、正方形或正六边形铺满地面,如果我们要同时用两种不同的正多边形铺满地面,可以设计出几种不同的组合方案?
问题解决:
猜想1:是否可以同时用正方形、正八边形两种正多边形组合铺满地面?
验证1并完成填空:在铺地面时,设围绕某一个点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意:可得方程①: ,
整理得②: ,
我们可以找到方程的正整数解为③: .
结论1:铺满地面时,在一个顶点周围围绕着④个正方形和⑤个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以铺满地面.
猜想2:是否可以同时用正三角形和正六边形两种正多边形组合铺满地面?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com