
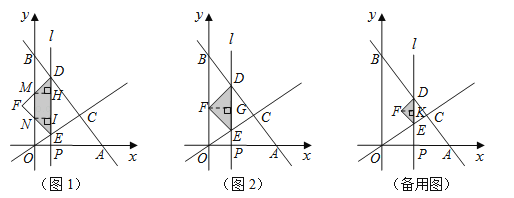
����Ŀ����ͼ1��ֱ��![]() �ֱ���x�ᡢy�ύ��A��B���㣬��ֱ��
�ֱ���x�ᡢy�ύ��A��B���㣬��ֱ��![]() ���ڵ�
���ڵ�![]() ��ƽ����y���ֱ��l��ԭ��O��������ÿ��1����λ���ȵ��ٶ���x������ƽ�ƣ���C��ʱֹͣ��ֱ��l�ֱ��߶�BC��OC��x���ڵ�D��E��P����DEΪб�������������ֱ��
��ƽ����y���ֱ��l��ԭ��O��������ÿ��1����λ���ȵ��ٶ���x������ƽ�ƣ���C��ʱֹͣ��ֱ��l�ֱ��߶�BC��OC��x���ڵ�D��E��P����DEΪб�������������ֱ��![]() ����ֱ��l���˶�ʱ��Ϊt(��)��
����ֱ��l���˶�ʱ��Ϊt(��)��
(1)��գ�k=____��b=____��
(2)��tΪ��ֵʱ����F��y����(��ͼ2��ʾ)��
(3)��![]() ��
��![]() �ص����ֵ����ΪS����ֱ��д��S��t�ĺ�����ϵʽ(��Ҫ��д������)����д��t��ȡֵ��Χ��
�ص����ֵ����ΪS����ֱ��д��S��t�ĺ�����ϵʽ(��Ҫ��д������)����д��t��ȡֵ��Χ��

���𰸡�(1)![]() ��4��(2)t=1��(3)S=��t��2��2��
��4��(2)t=1��(3)S=��t��2��2��
��������
��1�����ô���ϵ�����������k��b��ֵ��
��2����F��y����ʱ��F��DE�ľ������DE�ij���һ�����ݴ˼����з������t��ֵ��
��3����F��y��������Ҳ��������������������F��y������ʱ����Ӱ��������������ֱ������������IJ�����F��y����Ҳ�ʱ����Ӱ���־��ǡ�DEF����������������ε������ʽ������ú����Ľ���ʽ��
��1���ѣ�2��![]() ������y=��
������y=��![]() x+b������
x+b������![]() +b=
+b=![]() �������b=4��
�������b=4��
�ѣ�2��![]() ������y=kx����2k=
������y=kx����2k=![]() �������k=
�������k=![]() ��
��
�ʴ�Ϊ��![]() ��4��
��4��
��2���ɣ�1������ֱ�ߵĽ���ʽΪ��
y=��![]() x+4��y=
x+4��y=![]() x�����������OP=t����D��t����
x�����������OP=t����D��t����![]() t+4����E��t��
t+4����E��t��![]() t����
t����
��DE=��2t+4����FG��DE��G����FG=OP=t��
�ߡ�DEF�ǵ���ֱ����������FG��DE����FG=![]() DE����t=
DE����t=![]() ����2t+4���������t=1��
����2t+4���������t=1��
��3����0��t��1ʱ����ͼ1����S��DEF=![]() ����
����![]() t+4��
t+4��![]() t��
t��![]() ����
����![]() t+4��
t+4��![]() t��=
t��=![]() ����2t+4��2=��t��2��2����y�����߲����ǵ���ֱ�����������ױ��ϵĸ�����
����2t+4��2=��t��2��2����y�����߲����ǵ���ֱ�����������ױ��ϵĸ�����![]() ����
����![]() t+4��
t+4��![]() t����t=
t����t=![]() ����2t+4����t=2��2t�������������2��2t��2��
����2t+4����t=2��2t�������������2��2t��2��
S=��t��2��2����2��2t��2=��3t2+4t��
��1��t��2ʱ������ͼ������FK��DE�ڵ�K����
S=��t��2��2��
������������0��t��1ʱ��S=��3t2+4t����1��t��2ʱ��S=��t��2��2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����2��Ҫ˵����ABD����ACD�����������������ѡһ���������ѡ���ǣ� ��
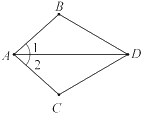
A. ��ADB����ADCB. ��B����CC. DB��DCD. AB��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
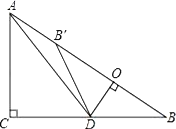
����Ŀ����ͼ����Rt��ABC�У���ACB=90����AC=6��BC=8����DΪ��CB�ϵ�һ�����㣨��D�����B�غϣ�����D��DO��AB������ΪO����B���ڱ�AB�ϣ������B����ֱ��DO�Գƣ�����DB����AD��
��1����֤����DOB�ס�ACB��
��2����ADƽ�֡�CAB�����߶�BD�ij���
��3������AB��DΪ����������ʱ�����߶�BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
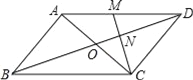
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD���ڵ�O��MΪAD�е㣬����CM��BD�ڵ�N����ON=1��
��1����BD�ij���
��2������DCN�����Ϊ2�����ı���ABNM�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABC�������������ֱ�ΪA��0����3����B��3����2����C��2����4���������������У�ÿ��С�����εı߳���1����λ���ȣ�
��1��������ABC����ƽ��6����λ�õ�����A1B1C1��
��2���Ե�CΪλ�����ģ��������л�����A2B2C2��ʹ��A2B2C2����ABCλ�ƣ�����A2B2C2����ABC��λ�Ʊ�Ϊ2��1����ֱ��д����A2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ�����ɸ���ͬ�ĺ�����Ϊ�˹��ƴ��к����������ijѧϰС����������ʵ�������ǽ�30��������С��״��ȫ��ͬ�İ���װ����������Ⱥ�����������һ��������ɫ���ٰ����Żش����������ظ�![]() �±��Ǽ��λ���ܺ�ͳ�Ƶ�������
�±��Ǽ��λ���ܺ�ͳ�Ƶ�������
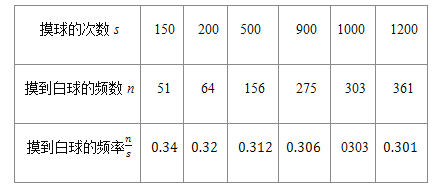
![]() �������������s�ܴ�ʱ�����������Ƶ�ʽ���ӽ�______ ��������ȥ��һ��������������ĸ�����______
�������������s�ܴ�ʱ�����������Ƶ�ʽ���ӽ�______ ��������ȥ��һ��������������ĸ�����______ ![]() ��ȷ��
��ȷ��![]() ��
��
![]() �Թ���ڴ��к����ж���ֻ��
�Թ���ڴ��к����ж���ֻ��
![]() ��������������������ͳ������ʷ���̸һ����ʾ��
��������������������ͳ������ʷ���̸һ����ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���һ����λ���ȣ���
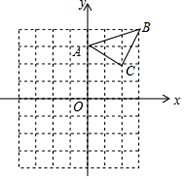
��1����ABC����ƽ��4����λ���ȵõ�����A1B1C1����C1�������� ��
��2���Ե�BΪλ�����ģ��������ڻ�����A2B2C2��ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2��1����C2�������� ��������ͼ�Σ�
��3����A2B2C2������� ƽ����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ű�������������ͼ��ʾ�ķ�����ֱ�ǣ���һ���������ϵȾ����13���ᣬȻ����3�����ࡢ4�����ࡢ5������ij���Ϊ�߳�����ľ����һ�������Σ�����һ���DZ���ֱ�ǣ��������ĵ����ǣ�������
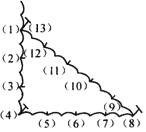
A. ֱ��������������ǻ���
B. �������ڽǺ͵���180��
C. ��������������߳���ƽ���͵��ڵ����߳���ƽ��
D. ��������������߳���ƽ���͵��ڵ����߳���ƽ������ô�����������ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
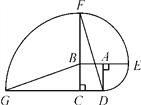
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊ1��������������![]() ��
��![]() ��
��![]() ��Բ�������ǵ�A��B��C.
��Բ�������ǵ�A��B��C.
(1)���D������Բ���˶�����G��������·�߳���
(2)�ж�ֱ��GB��DF��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com