
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
【答案】C
【解析】解析:选项A.用平方差公式法,应为x2y2-z2=(xy+z)·(xy-z),故本选项错误.
选项B.用提公因式法,应为-x2y+ 4xy-5y=- y(x2- 4x+5),故本选项错误.
选项C.用平方差公式法,(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1),故本选项正确.
选项D.用完全平方公式法,应为9-12a+4a2=(3-2a)2,故本选项错误.
故选C.
点睛:(1)完全平方公式: ![]() .
.
(2)平方差公式:(a+b)(a-b)= ![]() .
.
(3)常用等价变形: ![]()
![]() ,
,
![]() ,
,
![]() .
.
【题型】单选题
【结束】
10
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何图形很神奇,由一些多边形组成的图形中离不开边和顶点,它们之间有着很多奥秘等待我们去探索.先看下面一道有趣的关于顶点和边的题:如图所示,图①~图④都是平面图形.

(1)每个图中各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入下列表格中:

(2)根据(1)中的结论,推断出一个平面图形的顶点数、边数、区域数之间有什么关系(设顶点数为n).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
解:设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
【答案】(1)C;(2)不彻底,(x-2)4;(3)(x-1)4.
【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解;
试题解析:
(1)运用了C,两数和的完全平方公式;
(2)不彻底;
(x2-4x+4)2=(x-2)4
(3)设x2-2x=y.
(x2-2x)(x2-2x+2)+1
=y(y+2)+1
=y2+2y+1
=(y+1)2…………………………7分
=(x2-2x+1)2
=(x-1)4.
【题型】解答题
【结束】
24
【题目】乘法公式的探究及应用.
探究问题
图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2.

![]()
(1) (2)
(1)图1中长方形纸条的面积可表示为_______(写成多项式乘法的形式).
(2)拼成的图2阴影部分的面积可表示为________(写成两数平方差的形式).
(3)比较两图阴影部分的面积,可以得到乘法公式:____.
结论运用
(4)运用所得的公式计算:
![]() =________;
=________; ![]() =________.
=________.
拓展运用:
(5)计算: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
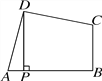
A. 3 B. 2![]() C. 3
C. 3![]() D. 3
D. 3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com