
如图所示,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙Oˊ与y轴正半轴交于点C,连接BC,AC。CD是半⊙Oˊ的切线,AD⊥CD于点D。

(1)求证:∠CAD =∠CAB;
(2)已知抛物线y=ax2+bx+c过A、B、C三点,AB=10,AC=2BC。
①求抛物线的解析式;
②判断抛物线的顶点E是否在直线CD上,并说明理由。
(1)证明见解析;(2)y=-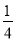 x2-
x2-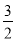 x+4;在,理由见解析.
x+4;在,理由见解析.
【解析】
试题分析:(1)连接O′C,由CD是⊙O的切线,可得O′C⊥CD,则可证得O′C∥AD,又由O′A=O′C,则可证得∠CAD=∠CAB;
(2)①首先证得△CAO∽△BCO,根据相似三角形的对应边成比例,可得OC2=OA•OB,又由tan∠CAO=tan∠CAD=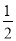 ,则可求得CO,AO,BO的长,然后利用待定系数法即可求得二次函数的解析式;
,则可求得CO,AO,BO的长,然后利用待定系数法即可求得二次函数的解析式;
②首先证得△FO′C∽△FAD,由相似三角形的对应边成比例,即可得到F的坐标,求得直线DC的解析式,然后将抛物线的顶点坐标代入检验即可求得答案;
试题解析:(1)证明:连接O′C,
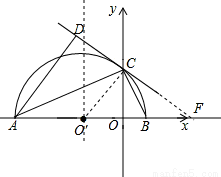
∵CD是⊙O′的切线,
∴O′C⊥CD,
∵AD⊥CD,
∴O′C∥AD,
∴∠O′CA=∠CAD,
∵O′A=O′C,
∴∠CAB=∠O′CA,
∴∠CAD=∠CAB;
(2)【解析】
①∵AB是⊙O′的直径,
∴∠ACB=90°,
∵OC⊥AB,
∴∠CAB=∠OCB,
∴△CAO∽△BCO,
∴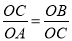 ,
,
即OC2=OA•OB,
∵tan∠CAO=tan∠CAD=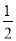 ,
,
∴AO=2CO,
又∵AB=10,
∴OC2=2CO(10-2CO),
解得CO1=4,CO2=0(舍去),
∴CO=4,AO=8,BO=2
∵CO>0,
∴CO=4,AO=8,BO=2,
∴A(-8,0),B(2,0),C(0,4),
∵抛物线y=ax2+bx+c过点A,B,C三点,
∴c=4,
由题意得: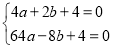 ,
,
解得: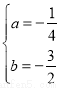 ,
,
∴抛物线的解析式为:y=-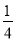 x2-
x2-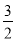 x+4;
x+4;
②设直线DC交x轴于点F,
∴△AOC≌△ADC,
∴AD=AO=8,
∵O′C∥AD,
∴△FO′C∽△FAD,
∴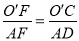 ,
,
∴O′F•AD=O′C•AF,
∴8(BF+5)=5(BF+10),
∴BF=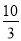 ,F(
,F(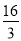 ,0);
,0);
设直线DC的解析式为y=kx+m,
则
 ,
,
解得: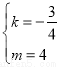 ,
,
∴直线DC的解析式为y=-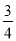 x+4,
x+4,
由y=-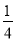 x2-
x2-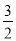 x+4=-
x+4=-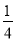 (x+3)2+
(x+3)2+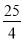 得顶点E的坐标为(-3,
得顶点E的坐标为(-3,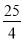 ),
),
将E(-3,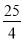 )代入直线DC的解析式y=-
)代入直线DC的解析式y=-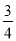 x+4中,
x+4中,
右边=-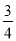 ×(-3)+4=
×(-3)+4=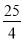 =左边,
=左边,
∴抛物线顶点E在直线CD上;
考点:二次函数综合题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:选择题
已知函数y=(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=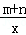 的图象可能是( )
的图象可能是( )
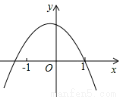
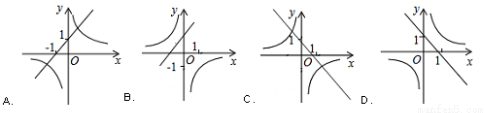
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:选择题
一元二次方程x2 +2x+4=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广西省九年级12月月考数学试卷(解析版) 题型:选择题
函数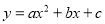 的图像如图所示,那么关于
的图像如图所示,那么关于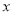 的方程
的方程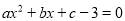 的根的情况是( )
的根的情况是( )
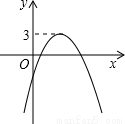
A.有两个不相等的实数根 B.有两个异号实数根
C.有两个相等的实数根 D.无实数根
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市永定丰田片区九年级上学期第三次月考数学试卷(解析版) 题型:解答题
某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加。某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80。设这种产品每天的销售利润为W元。
(1)求W与x之间的函数关系式。
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市永定丰田片区九年级上学期第三次月考数学试卷(解析版) 题型:填空题
一个口袋里放有三枚除颜色外都相同的棋子,其中有两枚是白色的,一枚是红色的。从中随机摸出一枚记下颜色,放回口袋搅匀,再从中随机摸出一枚记下颜色,两次摸出棋子颜色不同的概率是 。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年云南省九年级11月月考数学试卷(解析版) 题型:解答题
已知关于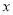 的方程
的方程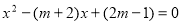 。
。
(1)求证:方程恒有两个不相等的实数根。
(2)若此方程的一个根为1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省七年级上学期期末考试数学试卷(解析版) 题型:选择题
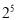 表示的意义是 ( )
表示的意义是 ( )
A.5个2相乘
B.5与2相乘
C.5个2相加
D.2个5相乘
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com