
【题目】电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,为方便大家识别与印刷,我把图乙中的0都标出来了,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙是张三玩游戏中的局部,图中有4个方块己确定是雷(方块上标有旗子),则图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有
.(请填入方块上的字母)
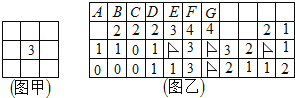
【答案】B、D、F、G.
【解析】
根据扫雷规则逐个判断.
图乙中最左边的“1”和最右边的“1”,可得如下推断:
由第三行最左边的“1”,可得它的上方必定是雷.
结合B下方的“2”,可得最左边的A、B对应的方格中有一个雷;
同理可得最右边的“4”周围4个方格中有3个雷,中间D、E对应方格中有一个雷;
由于B下方的“2”和第二行最右边的“2”,它们周围的雷已经够数,
所以C对应的方格肯定不是雷.
进行下一步推理:
因为C对应的方格不是雷,所以C下方“2”的左上、右上的方格,即B、D都是雷;
而B下方的“2”的周围的雷也已经够数,所以A对应的方格也不是雷.
因为D下方的“2”,它的周围的雷已经够数,可得E对应的方格不是雷,
根据F下方的“4”周围应该有4个雷,结合E不是雷,可得F、G对应的方格都是雷.
综上所述,A、C、E对应的方格不是雷,且B、D、F、G对应的方格是雷.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.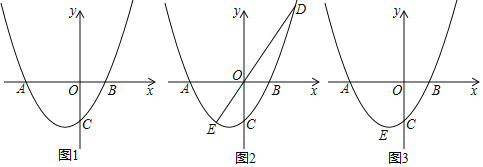
(1)如图1,分别求![]() 的值;
的值;
(2)如图2,点![]() 为第一象限的抛物线上一点,连接
为第一象限的抛物线上一点,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 为第一象限的抛物线上一点,过点
为第一象限的抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 为第二象限的抛物线上一点,且点
为第二象限的抛物线上一点,且点![]() 与点
与点![]() 关于抛物线的对称轴对称,连接
关于抛物线的对称轴对称,连接![]() ,设
,设![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为第三象限的抛物线上一点,分别连接
为第三象限的抛物线上一点,分别连接![]() ,满足
,满足![]() ,
,![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
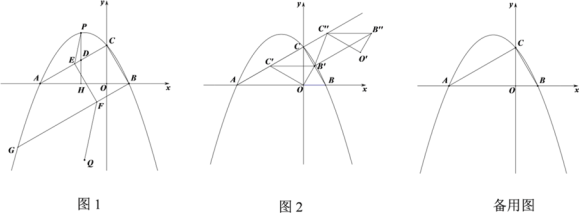
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
(1)如图1,求直线BC的解析式;
(2)如图1,线段AC上方抛物线上有一动点P,PD⊥x轴于点H,交线段AC于点D,直线BG∥AC,交抛物线于点G,点F是直线BC上一动点,FE∥BC交AC于点E,点Q是点A关于直线BG的对称点,连接PE、QF.当线段PD取最大值时,求PE+EF+QF的最小值及点E的坐标;
(3)如图2,将△BOC绕点O逆时针旋转至△B′O C′的位置,点B、C的对应点分别为点B′、C′,点B′恰好落在BC上.将△B′O C′沿直线AC平移,得到△B′′O ′ C′′,点B′、C′、O的对应点分别为点B′′、C′′、O ′,连接B ′ B′′、B ′C′′,△B ′B′′C′′是否能为等腰三角形?若能,请直接写出所有符合条件的C′′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
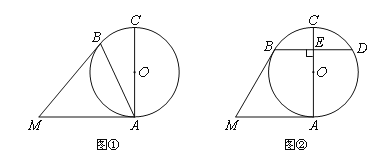
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,E为边BC上的一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMNP和点同时停止运动.设运动时间为t秒,解答问题:

(1)在整个运动过程中,当点G在线段AE上时,求t的值;
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形,若存在,求出t的值;若不存在,说明理由;
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t的函数关系式以及自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AC为直径的O恰为△ABC的外接圆,∠ABC的平分线交O于点D,过点D作DE∥AC交BC的延长线于点E
(1)求证:DE是⊙O的切线;
(2)若AB=4![]() ,BC=2
,BC=2![]() ,求DE的长.
,求DE的长.
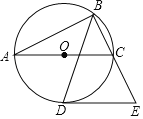
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
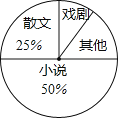
(1)计算m= ;
(2)在扇形统计图中,“其他”类所占的百分比为 ;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com