
【题目】已知,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.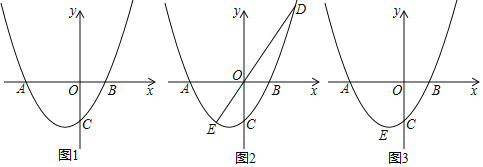
(1)如图1,分别求![]() 的值;
的值;
(2)如图2,点![]() 为第一象限的抛物线上一点,连接
为第一象限的抛物线上一点,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 为第一象限的抛物线上一点,过点
为第一象限的抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 为第二象限的抛物线上一点,且点
为第二象限的抛物线上一点,且点![]() 与点
与点![]() 关于抛物线的对称轴对称,连接
关于抛物线的对称轴对称,连接![]() ,设
,设![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为第三象限的抛物线上一点,分别连接
为第三象限的抛物线上一点,分别连接![]() ,满足
,满足![]() ,
,![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将点A、B的坐标代入抛物线表达式,即可求解;
(2)作![]() 轴于K,
轴于K,![]() 轴于L,OD=3OE,则OL=3OK,DL=3KE,设点E的横坐标为t,则点D的横坐标为-3t,则点E、D的坐标分别为:(t,
轴于L,OD=3OE,则OL=3OK,DL=3KE,设点E的横坐标为t,则点D的横坐标为-3t,则点E、D的坐标分别为:(t,![]() )、(-3t,-
)、(-3t,-![]() +3t+
+3t+![]() ),即可求解;
),即可求解;
(3)设点![]() 的横坐标为
的横坐标为![]() ,可得PH=
,可得PH=![]() m2+m-
m2+m-![]() ,过
,过![]() 作EF∥y轴交
作EF∥y轴交![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() ,TE=PH+YE=
,TE=PH+YE=![]() m2+m-
m2+m-![]() +2=
+2=![]() (m+1)2,tan∠AHE=
(m+1)2,tan∠AHE=![]() ,tan∠PET=
,tan∠PET=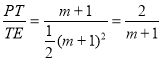 ,而∠AHE+∠EPH=2α,故∠AHE=∠PET=∠EPH=α,PH=PQtanα,即
,而∠AHE+∠EPH=2α,故∠AHE=∠PET=∠EPH=α,PH=PQtanα,即![]() m2+m-
m2+m-![]() =(2m+2)×
=(2m+2)×![]() ,解得:m=2
,解得:m=2![]() -1,故YH=m+1=2
-1,故YH=m+1=2![]() ,PQ=4
,PQ=4![]() ,点P、Q的坐标分别为:(2
,点P、Q的坐标分别为:(2![]() -1,4)、(-2
-1,4)、(-2![]() -1,4),tan∠YHE=
-1,4),tan∠YHE=![]() ,tan∠PQH=
,tan∠PQH=![]() ;证明△PMH≌△WNH,则PH=WH,而QH=2PH,故QW=HW,即W是QH的中点,则W(-1,2),再根据待定系数法即可求解.
;证明△PMH≌△WNH,则PH=WH,而QH=2PH,故QW=HW,即W是QH的中点,则W(-1,2),再根据待定系数法即可求解.
解:(1)把![]() 、
、![]() 分别代入
分别代入![]() 得:
得:
 ,解得
,解得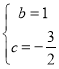 ;
;
(2)如图2,由(1)得![]() ,作
,作![]() 轴于K,
轴于K,![]() 轴于L,
轴于L,
∴EK∥DL,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,
,![]() ,
,
∴![]() 的横坐标为
的横坐标为![]() ,分别把
,分别把![]() 和
和![]() 代入抛物线解析式得
代入抛物线解析式得![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() (舍),
(舍),![]() ,
,
∴![]() .
.
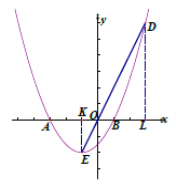
(3)如图3,设点![]() 的横坐标为
的横坐标为![]() ,把
,把![]() 代入抛物线得
代入抛物线得![]() ,
,
∴![]() .
.
过![]() 作EF∥y轴交
作EF∥y轴交![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() ,∴
,∴![]() 轴.
轴.
∵点![]() 与点
与点![]() 关于抛物线的对称轴对称,∴PQ∥x轴,
关于抛物线的对称轴对称,∴PQ∥x轴,![]() ,
,
∴![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
又∵![]() 轴,∴ET∥PH,∴
轴,∴ET∥PH,∴![]() ,
,
∴![]() ,∴四边形
,∴四边形![]() 为矩形,
为矩形,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
, ,
,
∴![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() 解得
解得![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() ,
,
把![]() 代入抛物线得
代入抛物线得![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ∴
∴![]() .
.
若![]() 交
交![]() 于点
于点![]() ,
,
∵NF∥PE,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
作WS∥PQ,交![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() ,
,
∴△WSH∽△QPH,∴![]() .
.
∵![]() ∴
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
设![]() 的解析式为
的解析式为![]() ,把
,把![]() 、
、![]() 代入得,
代入得,
 解得
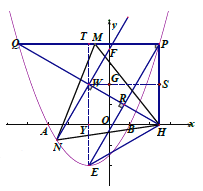
解得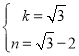 ,∴
,∴![]() .
.
∵FN∥PE,∴设![]() 的解析式为
的解析式为![]() ,把
,把![]() 代入得
代入得![]() ,
,
∴![]() 的解析式为
的解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】期中考试中,A,B,C,D,E五位同学的数学、英语成绩有如表信息:
A | B | C | D | E | 平均分 | 中位数 | |
数学 | 71 | 72 | 69 | 68 | 70 |
|
|
英语 | 88 | 82 | 94 | 85 | 76 |
|
|
(1)完成表格中的数据;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩﹣平均成绩)÷成绩方差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
查看答案和解析>>
科目:初中数学 来源: 题型:
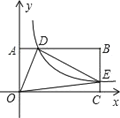
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
A.![]() B.9C.
B.9C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车驾驶员坐在驾驶座位上,其视线观察不到的地方叫“汽车盲区”.如图是一辆汽车的“车头盲区”示意图,其中AC⊥BC,DE⊥BC,驾驶员所处位置的高度AC为1.4米,驾驶员座位AC与车头DE之间距离为2米,当驾驶员从A点观察车头D点时,其视线的俯角为12°,点A、D、B在同一直线上.
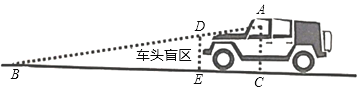
(1)请直接写出∠ABC的度数;
(2)求“车头盲区”点B、E之间的距离.(结果精确到0.1米)参考数据:sin12°=0.20,cas12°=0.99,tan12°=0.21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,亮亮、悦悦两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,亮亮到达B地后立即以另一速度按原路返回.如图是两人离A地的距离y(米)与悦悦运动的时间x(分)之间的函数图象,则亮亮到达A地时,悦悦还需要____________分到达A地.
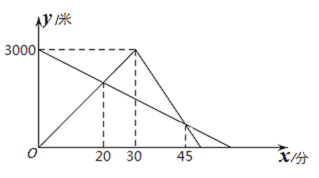
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,为方便大家识别与印刷,我把图乙中的0都标出来了,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙是张三玩游戏中的局部,图中有4个方块己确定是雷(方块上标有旗子),则图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有
.(请填入方块上的字母)
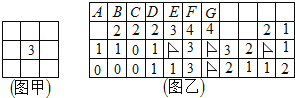
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(6,0),B(0,8),动点C从点B出发,沿射线BO方向以每秒1个单位的速度运动,同时动点D从点A出发,沿x轴正方向以每秒1个单位的速度运动,连结CD交直线AB于点E,设点C运动的时间为t秒.

(1)当点C在线段BO上时,
①当OC=5时,求点D的坐标;
②问:在运动过程中,![]() 的值是否为一个不变的值?若是,请求出
的值是否为一个不变的值?若是,请求出![]() 的值,若不是,请说明理由?
的值,若不是,请说明理由?
(2)是否存在t的值,使得△BCE与△DAE全等?若存在,请求出所有满足条件的t的值;不存在,请说明理由.
(3)过点E作AB的垂线交x轴于点H,交y轴于点G(如图),当以点C为圆心,CE长 为半径的⊙C经过点G或点H时,请直接写出所有满足条件的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com