
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B������B��ֱ�߽�x����C����
��x�ύ�ڵ�A����y�ύ�ڵ�B������B��ֱ�߽�x����C����![]() ���Ϊ10.
���Ϊ10.
��1�����C�����꼰ֱ��BC�Ľ���ʽ��
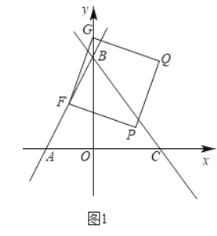
��2����ͼ1�����FΪ�߶�AB�е㣬��GΪy����һ���㣬����FG����FGΪ����FG�Ҳ���������FGQP����G����˶������У�������Q����ֱ��BC��ʱ�����G�����ꣻ
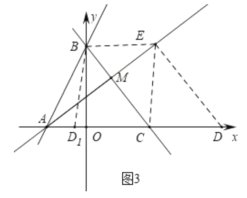
��3����ͼ2����MΪ�߶�BC��һ�㣬������![]() ����EΪֱ��AM��һ���㣬��x�����Ƿ���ڵ�D��ʹ�Ե�D��E��B��CΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵������.
����EΪֱ��AM��һ���㣬��x�����Ƿ���ڵ�D��ʹ�Ե�D��E��B��CΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵������.

���𰸡���1��C(3,0)��y=![]() ����2��G������ΪG(0,
����2��G������ΪG(0,![]() ),G(0,
),G(0,![]() )����3��D������Ϊ(
)����3��D������Ϊ(![]() ,0)�� (
,0)�� (![]() ,0) ��(
,0) ��(![]() ,0)
,0)
��������
��1�����������������ʽ�����C���꣬�����ô���ϵ���������ʽ���ɣ�
��2��������������ٵ�n��2ʱ����ͼ2-1�У���Q����BC�ϣ���G����ֱ��ƽ����x�ᣬ����F��Q����ֱ�ߵĴ��ߣ�����ֱ�ΪM��N�����Q(n-2��n-1).�ڵ�n��2ʱ����ͼ2-2��ͬ���ɵ�Q(2-n��n+1)�����ô���ϵ������⼴�ɣ�
��3�����������������ʽ���M���꣬�Ӷ����ֱ��AM�Ľ���ʽ����BE��OC��AM��E����CD=BEʱ�ɵ��ı���BCDE���ı���BECD1��ƽ���ı��Σ�Ȼ���һ���ó���������.
��1����ֱ��y=2x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��
��A(-2,0)��B(0,4)��
��OA=2��OB=4��
��S��ABC=![]() ACOB=10��
ACOB=10��
��AC=5��
��OC=3��
��C(3,0)��
��ֱ��BC����ʽΪy=kx+b��
��3k+b=0��b=4��
��k=![]() ��
��
��ֱ��BC����ʽΪy=![]() ��
��
��2����FA=FB��A(-2,0)��B(0,4)��
��F(-1,2)����G(0,n)��
��n��2ʱ����ͼ2-1��ʾ����Q����BC��ʱ����G��ֱ��ƽ����x�ᣬ����F��Q����ֱ�ߵĴ��ߣ�����ֱ�ΪM��N��
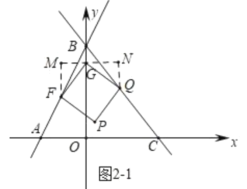
���ı���FGQP�������Σ�
����FMG����GNQ��
��MG=NQ=1��FM=GN=n-2��
��Q(n-2��n-1)��
��Q����ֱ��y=![]() �ϣ�
�ϣ�
��n-1=![]() ��
��
��n=![]() ��
��
��G(0,![]() ),
),
��n��2ʱ����ͼ2-2��ͬ���ɵã�Q(2-n��n+1)��

��Q����ֱ��y=![]() �ϣ�
�ϣ�
��n+1=![]() ��
��
��n=![]() ��
��
��G(0,![]() ),
),
����������G������ΪG(0,![]() ),G(0,
),G(0,![]() )��
)��
��3����ͼ3����M(m,![]() )��
)��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���![]() ��
��
��M(![]() ,
,![]() )��
)��
��ֱ��AM�Ľ���ʽΪ![]() ��
��
��BE��OC��ֱ��AM��E����ʱE(![]() ,4)��
,4)��
��CD=BEʱ���ı���BCDE���ı���BECD1��ƽ���ı��Σ�
�ɵã�D(![]() ,0)��D1(
,0)��D1(![]() ,0)��
,0)��
���ݶԳ��Կɵ�D����A�ĶԳƵ�D2(![]() ,0)Ҳ����������
,0)Ҳ����������
����������D��������(![]() ,0)�� (
,0)�� (![]() ,0) ��(
,0) ��(![]() ,0)
,0)



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����⾺�»����6��ʽ������С����ͬ������������ֻ��һ������������������ѡ�ֽ��ش�5����Ŀ��ÿ���һ���⣬�����˾ʹ�6��������ȥ��һ�������ӣ���ѡ��һ���������ȡ������Ĵ����ʸ�ʣ�µ�������ѡȡһ�����ӣ�
��1��һ��ѡ�ִ����4���⣬����ѡ�в�����������ӵĸ��ʣ�
��2����֪һ��ѡ��ѡ�в�����������ӵĸ���Ϊ![]() ����������˼����⣿
����������˼����⣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�С����������ı߳�Ϊ 1����λ���ȣ���ABC���������������ֱ�ΪA����3��4����B����5��2����C����2��1����
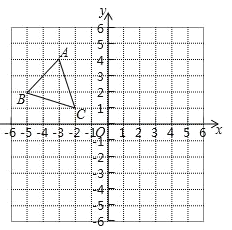
��1������![]() ����
����![]() ��ԳƵ�ͼ��
��ԳƵ�ͼ��![]() ��д����
��д����![]() �����ꣻ
�����ꣻ
��2����![]() �Ƶ�O��ʱ����ת
�Ƶ�O��ʱ����ת![]() ��������ת���
��������ת���![]() ,��д����
,�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ����ڡ����ҹ��Ŵ���������ѧ�����������������е�һ�����⣬������Բ�ģ����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ⼸�Σ������ִ�����ѧ���Ա����ǣ�����ͼ��CDΪ��O��ֱ������AB��CD����ΪE��CE=1�磬AB=10�磬��ֱ��CD�ij����������⣬CD��Ϊ�� ��

A��12�� B��13�� C��24�� D��26��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����70���꣬ijУ���а༶��ӽ�����������У����Ұ��㣬�й��������質����������Һ��ҵ���������ֱ�����ĸA��B��C���α�ʾ����������������ʱ����A��B��C��������ĸ�ֱ�д��3��������Ŀ�Ƭ�����ϣ�ϴ�Ⱥ��������·��������ϣ��ˣ�1�����ȴ��������ȡһ�ſ�Ƭ���Żغ�ϴ�ȣ����ɰˣ�2�������������ȡһ�ſ�Ƭ�����и�ӽ������
��1���ˣ�1������и������Һ��ҵ�������ĸ�����__________��
��2�����û���״ͼ���б��ķ�����ʾ���п��ܵĽ����������ˣ�1����Ͱˣ�2������в�ͬ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ����
����![]() �ύ��
�ύ��![]() ��
��![]() ��
��![]() ֮�䣨�����������㣩�˶����������ĸ����ۣ�
֮�䣨�����������㣩�˶����������ĸ����ۣ�
����������![]() �����һ��������
�����һ��������![]() ��
��
�ڵ�![]() ��
��![]() ���������ϣ�������
���������ϣ�������![]() ����
����![]() ��
��
�۳�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
��ϵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() .
.
����������������ȷ���۵�����ǣ� ��
A.�٢ڢ�B.�ڢۢ�C.�٢�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() ��һ���Ե�
��һ���Ե�![]() Ϊ�����
Ϊ�����![]() ���Ƶ�
���Ƶ�![]() ��ת���ǵ�������
��ת���ǵ�������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
��![]() ������
������![]() .
.
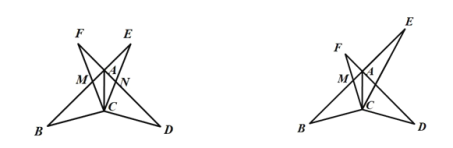
��1����![]() ��ת�Ĺ����У���
��ת�Ĺ����У���![]() ʱ����ͼ1.��֤��
ʱ����ͼ1.��֤��![]() ��
��
��2����![]() ��ת�Ĺ����У���
��ת�Ĺ����У���![]() ʱ����ͼ2�����
ʱ����ͼ2�����![]() ��
��![]() ���õ�ʽ��ʾ�߶�
���õ�ʽ��ʾ�߶�![]() ��
��![]() ֮���������ϵ����֤��.
֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB��5cm��BC��10cm����P�ӵ�A��������AB�����B��ÿ��1cm���ٶ��ƶ���ͬʱ��Q�ӵ�B������BC�����C��ÿ��2cm���ٶ��ƶ���P��Q�����ڷֱ�B��C����ʱ��ֹͣ�ƶ����������ƶ���ʱ��Ϊt�룬����������⣺
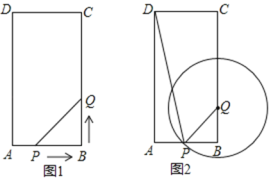
��1����ͼ1����tΪ����ʱ����PBQ���������4cm2��
��2����ͼ2����QΪԲ�ģ�PQΪ�뾶����Q�����˶������У��Ƿ����������tֵ��ʹ��Q�������ı���DPQC��һ�ߣ�������ڵ�ֱ�ߣ����У������ڣ����tֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�Ķ��������ֱ�ΪA��2��2����B��1��0����C��3��1����
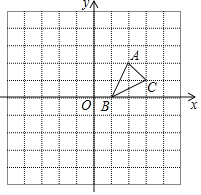
��1��������ABC����x��ԳƵ���A1BC1��д����C1������Ϊ�� ����
��2��������ABC��ԭ��O��ʱ����ת90������A2B1C2��д����C2������Ϊ�� ����
��3���ڣ�1������2���Ļ����ϣ�ͼ�е���A1BC1����A2B1C2���ڵ��� �����ĶԳƣ�
��4�����Ե�D��A��C��BΪ������ı���Ϊ���Σ�ֱ��д����D������Ϊ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com