
【题目】如图,![]() ,
,![]() ,
,![]() ,一个以点
,一个以点![]() 为顶点的
为顶点的![]() 角绕点
角绕点![]() 旋转,角的两边与
旋转,角的两边与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,与
,与![]() 、
、![]() 的延长线交于点
的延长线交于点![]() 、
、![]() ,连接
,连接![]() .
.
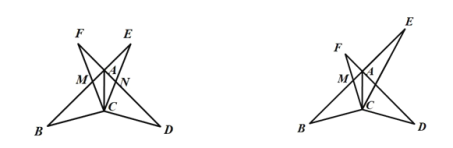
(1)在![]() 旋转的过程中,当
旋转的过程中,当![]() 时,如图1.求证:
时,如图1.求证:![]() ;
;
(2)在![]() 旋转的过程中,当
旋转的过程中,当![]() 时,如图2,如果
时,如图2,如果![]() ,
,![]() ,用等式表示线段
,用等式表示线段![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)证明见解析;(2)AE·AF=2,证明见解析.
【解析】
(1)先证明△ABC≌△ADC,然后再证明△ACF≌△ACE即可得;
(2)过点C作CG⊥AB于点G,先求出AC的长,再证明△ACF∽△AEC,根据相似三角形的性质即可得.
(1)∵AB=AD,BC=CD,AC=AC,∴△ABC≌△ADC,
∴∠BAC=∠DAC=45°,∴180°-∠BAC=180°-∠DAC,∴∠FAC=∠EAC=135°,
又∵∠FCA=∠ECA,AC=AC
∴△ACF≌△ACE,
∴AE=AF;
(2)AE·AF=2,证明如下:
过点C作CG⊥AB于点G,则∠BGC=∠AGC=90°,

∵∠B=30°,∴CG=![]() BC=1,
BC=1,
∵∠BAC=45°,∴AC=![]() =
=![]()
∵∠FAC=∠EAC=135°,∴∠ACF+∠F=45°,
又∵∠ACF+∠ACE=45°,∴∠F=∠ACE,
∴△ACF∽△AEC,
∴![]() ,
,
故AC= AE·AF
∴AE·AF=2


科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
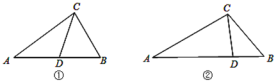
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆/小时)指单位时间内通过道路指定断面的车辆数;速度
(辆/小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米/小时)指通过道路指定断面的车辆速度,密度
(千米/小时)指通过道路指定断面的车辆速度,密度![]() (辆/千米)指通过道路指定断面单位长度内的车辆数.
(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度 | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量 | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确的是____.(只填上正确答案的序号)
关系最准确的是____.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]() .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() 满足
满足![]() .请结合(1)中选取的函数关系式继续解决下列问题.
.请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵;
在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离![]() (米)均相等,求流量
(米)均相等,求流量![]() 最大时
最大时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
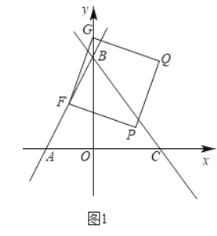
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点B,过点B的直线交x轴于C,且
与x轴交于点A,与y轴交于点B,过点B的直线交x轴于C,且![]() 面积为10.
面积为10.
(1)求点C的坐标及直线BC的解析式;
(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作正方形FGQP,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;
(3)如图2,若M为线段BC上一点,且满足![]() ,点E为直线AM上一动点,在x轴上是否存在点D,使以点D、E、B、C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
,点E为直线AM上一动点,在x轴上是否存在点D,使以点D、E、B、C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线的表达式为
中,抛物线的表达式为![]() ,线段AB的两个端点分别为A(1,2),B(3,2)
,线段AB的两个端点分别为A(1,2),B(3,2)
(1)若抛物线经过原点,求出![]() 的值;
的值;
(2)求抛物线顶点C的坐标(用含有m的代数式表示);
(3)若抛物线与线段AB恰有一个公共点,结合函数图象,求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.
(1)证明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的长,

查看答案和解析>>
科目:初中数学 来源: 题型:
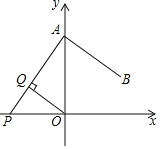
【题目】如图,在平面直角坐标系xOy中,点A(0,6),点B(4,3),P是x轴上的一个动点.作OQ⊥AP,垂足为Q,则点Q到直线AB的距离的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的计算器,购进时的单价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是600个,而销售单价每上涨1元,就会少售出10个.
(1)不妨设该种品牌计算器的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y个和销售该品牌计算器获得利润w元,并把结果填写在表格中:
销售单价(元) | x(x>30) |
销售量y(个) |
|
销售计算器获得利润w(元) |
|
(2)在第(1)问的条件下,若计算器厂规定该品牌计算器销售单价不低于35元,且商场要完成不少于500个的销售任务,求:商场销售该品牌计算器获得最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠B=90°,点D为线段BC上一个动点(不与点B,C重合),连接AD,将线段AD绕点D顺时针旋转90°得到线段DE,连接EC.
(1)①依题意补全图1;
②求证:∠EDC=∠BAD;
(2)①小方通过观察、实验,提出猜想:在点D运动的过程中,线段CE与BD的数量关系始终不变,用等式表示为 ;
②小方把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点E作EF⊥BC,交BC延长线于点F,只需证△ADB≌△DEF.
想法2:在线段AB上取一点F,使得BF=BD,连接DF,只需证△ADF≌△DEC.
想法3:延长AB到F,使得BF=BD,连接DF,CF,只需证四边形DFCE为平行四边形.
……
请你参考上面的想法,帮助小方证明(2)①中的猜想.(一种方法即可)
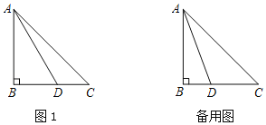
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com