
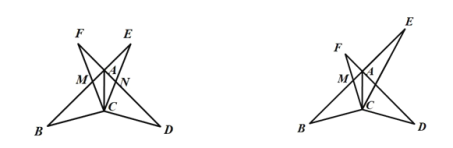
����Ŀ����ͼ���ڡ�ABC�У�AB��BC����B��90�㣬��DΪ�߶�BC��һ�����㣨�����B��C�غϣ�������AD�����߶�AD�Ƶ�D˳ʱ����ת90��õ��߶�DE������EC.
��1���������ⲹȫͼ1��
����֤����EDC����BAD;
��2����С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У��߶�CE��BD��������ϵʼ�ղ��䣬�õ�ʽ��ʾΪ�� ����
��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������E��EF��BC����BC�ӳ����ڵ�F��ֻ��֤��ADB�ա�DEF��
�뷨2�����߶�AB��ȡһ��F��ʹ��BF��BD������DF��ֻ��֤��ADF�ա�DEC��
�뷨3���ӳ�AB��F��ʹ��BF��BD������DF��CF��ֻ��֤�ı���DFCEΪƽ���ı��Σ�
����
����ο�������뷨������С��֤��(2)���еIJ��룮��һ�ַ������ɣ�
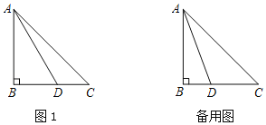
���𰸡���1���ټ������ڼ�������2���ٲ��룺CE��![]() BD�ڼ�����
BD�ڼ�����
��������
��1���������ⲹȫͼ�μ��ɣ����ɽǵĹ�ϵ���ɵó����ۣ�
��2������ȫ�������κ��ɶ����ɲ���CE=![]() BD��
BD��
���뷨1������E��EF��BC����BC�ӳ����ڵ�F��֤����ADB�ա�DEF���ó�AB=DF��BD=EF��֤��CF=BD=EF���ó���CEF�ǵ���ֱ�������Σ����ɵó����ۣ�
�뷨2�����߶�AB��ȡһ��F��ʹ��BF=BD������DF��֤��AF=DC��֤����ADF�ա�DEC���ó�CE=DF=![]() BD���ɣ�
BD���ɣ�
�뷨3���ӳ�AB��F��ʹ��BF=BD������DF��CF��֤����ABD�ա�CBF���ó�AD=CF����BAD=��BCF����֤���ı���DFCEΪƽ���ı��Σ����ɵó����ۣ�
��1������ȫ��ͼ����ͼ1��ʾ��

�ڡߡ�ADE����B��90�������EDC+��ADB����BAD+��ADB��90����
���EDC����BAD��
��2�������룺CE��![]() BD��
BD��
�ʴ�Ϊ��CE��![]() BD��
BD��
���뷨1��
֤��������E��EF��BC����BC�ӳ����ڵ�F����ͼ2��ʾ��
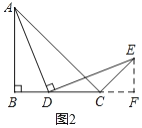
���F��90�������B����F��
����ADB����DEF��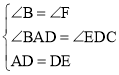 ��
��
���ADB�ա�DEF��AAS������AB��DF��BD��EF��
��AB��BC����DF��BC����DC+CF��BD+DC��
��CF��BD��EF�����CEF�ǵ���ֱ�������Σ�
��CE��![]() CF��
CF��![]() BD��
BD��
�뷨2��
֤�������߶�AB��ȡһ��F��ʹ��BF��BD������DF����ͼ3��ʾ��
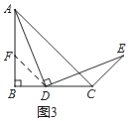
�ߡ�B��90����AB��BC��
��DF��![]() BD��
BD��
��AB��BC��BF��BD��
��AB��BF��BC��BD��
��AF��DC��
����ADF����DEC��
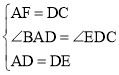 ��
��
���ADF�ա�DEC��SAS����
��CE��DF��![]() BD��
BD��
�뷨3��
֤�����ӳ�AB��F��ʹ��BF��BD������DF��CF����ͼ4��ʾ��

�ߡ�B��90������DF��![]() BD��
BD��
��Rt��ABD��Rt��CBF��
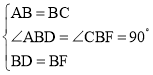 ��
��
���ABD�ա�CBF��SAS����
��AD��CF����BAD����BCF��
��AD��DE����DE��CF��
�ߡ�EDC����BAD�����EDC����BCF��
��DE��CF��
���ı���DFCEΪƽ���ı��Σ�
��CE��DF��![]() BD��
BD��


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��
��![]() ��һ���Ե�
��һ���Ե�![]() Ϊ�����
Ϊ�����![]() ���Ƶ�
���Ƶ�![]() ��ת���ǵ�������
��ת���ǵ�������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
��![]() ������
������![]() .
.
��1����![]() ��ת�Ĺ����У���
��ת�Ĺ����У���![]() ʱ����ͼ1.��֤��
ʱ����ͼ1.��֤��![]() ��
��
��2����![]() ��ת�Ĺ����У���
��ת�Ĺ����У���![]() ʱ����ͼ2�����
ʱ����ͼ2�����![]() ��
��![]() ���õ�ʽ��ʾ�߶�
���õ�ʽ��ʾ�߶�![]() ��
��![]() ֮���������ϵ����֤��.
֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y��![]() ��ͼ����ͼ��ʾ�����½��ۣ��ٳ���m����2������A����1��h����B��2��k����ͼ���ϣ���h��k����y��x���������С������P��x��y����ͼ���ϣ���P'����x����y��Ҳ��ͼ���ϣ�������ȷ���ǣ�������
��ͼ����ͼ��ʾ�����½��ۣ��ٳ���m����2������A����1��h����B��2��k����ͼ���ϣ���h��k����y��x���������С������P��x��y����ͼ���ϣ���P'����x����y��Ҳ��ͼ���ϣ�������ȷ���ǣ�������
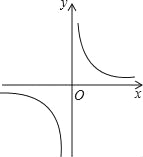
A. �٢�B. �ۢ�C. �ڢ�D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�Ķ��������ֱ�ΪA��2��2����B��1��0����C��3��1����
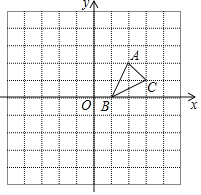
��1��������ABC����x��ԳƵ���A1BC1��д����C1������Ϊ�� ����
��2��������ABC��ԭ��O��ʱ����ת90������A2B1C2��д����C2������Ϊ�� ����
��3���ڣ�1������2���Ļ����ϣ�ͼ�е���A1BC1����A2B1C2���ڵ��� �����ĶԳƣ�
��4�����Ե�D��A��C��BΪ������ı���Ϊ���Σ�ֱ��д����D������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��
��![]() ������
������![]() ��.
��.
��1������![]()
![]() �����������ͼ���ϣ���
�����������ͼ���ϣ���![]() ��ֵ;
��ֵ;
��2�������������ͼ���ÿһ����֧�ϣ�![]() ��
��![]() �������������
�������������![]() ��ȡֵ��Χ;
��ȡֵ��Χ;
��3����![]() �����жϵ�
�����жϵ�![]()
![]() �Ƿ������������ͼ���ϣ���˵������.
�Ƿ������������ͼ���ϣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǡ������ǰ廭Բ�����ߡ��Ļ�ͼ������
��ͼ1����֪Բ��һ��A������A���Բ�����ߣ�
![]()

��������1����ͼ2�������ǰ��ֱ�Ƕ������Բ����һ��C�����A���غϣ�����ʹ��һֱ�DZ߾�����A����һ��ֱ�DZ���Բ����B�㣬����AB��
��2����ͼ3�������ǰ��ֱ�Ƕ������A�غϣ�ʹһ��ֱ�DZ߾�����B��������һ��ֱ�DZ����ڵ�ֱ��AD��
����ֱ��AD���ǹ���A��Բ�����ߣ�
��ش𣺸û�ͼ��������_______________________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽������ȫ�д��Ĺ���������̶ȣ�ij��ѧ��ѧ��ȤС����ȫ�мס����������ڽ����˵���ͳ�ƣ�����������Ϊ�����⣬һ�㣬���⣬�dz��������࣬���ա�������ȫ���ʾ��õ����в�������ͳ��ͼ��

����ͼ����Ϣ������������⣺
��1����˴ε����н��ܵ����������
��2����˴ε����н��Ϊ�dz������������
��3����ȤС�����ӵ�����Ϊ�������4λ���������ѡ��2λ���лطã���֪4λ��������2λ���Լ�������2λ���������������б����û���״ͼ�ķ������ѡ�����������Լ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
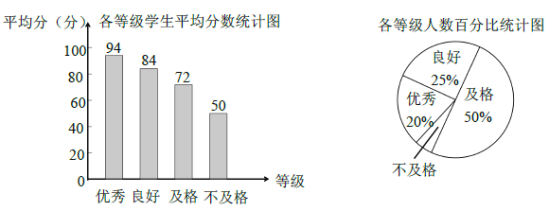
����Ŀ������ѧ�����ʽ��������涨ѧ�����ʽ����ȼ���Ϊ��90�ּ�����Ϊ���㣻80�֡�89��Ϊ���ã�60�֡�79��Ϊ����59�ּ�����Ϊ������. ijУ�Ӿ��꼶ѧ���������ȡ��![]() ��ѧ�����������ʲ��ԣ��÷��������ͼ.
��ѧ�����������ʲ��ԣ��÷��������ͼ.
��1���ڳ�ȡ��ѧ���в�����������ռ�İٷֱ��� ������Բ�ĽǶ���Ϊ ��.
��2��С�������·����������ȡ��ѧ��ƽ���÷��ǣ�![]() . ������ѧ��ͳ��֪ʶ�ж�С���ļ����Ƿ���ȷ��������ȷ���������ȷ���.
. ������ѧ��ͳ��֪ʶ�ж�С���ļ����Ƿ���ȷ��������ȷ���������ȷ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com