
����Ŀ����ͼ����ABC�Ķ��������ֱ�ΪA��2��2����B��1��0����C��3��1����
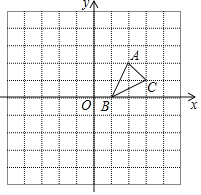
��1��������ABC����x��ԳƵ���A1BC1��д����C1������Ϊ�� ����
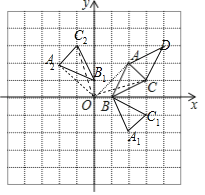
��2��������ABC��ԭ��O��ʱ����ת90������A2B1C2��д����C2������Ϊ�� ����
��3���ڣ�1������2���Ļ����ϣ�ͼ�е���A1BC1����A2B1C2���ڵ��� �����ĶԳƣ�
��4�����Ե�D��A��C��BΪ������ı���Ϊ���Σ�ֱ��д����D������Ϊ�� ����
���𰸡���1����3����1������2������1��3������3����![]() ��
��![]() ������4����4��4����
������4����4��4����
��������
��1�����ù���x�����������д��A1��C1�����꣬Ȼ����㼴�ɣ���2�����������ص����ת�����ʣ�д����A��B��C�Ķ�Ӧ��![]() ��
��![]() ��
��![]() ���Ӷ��õ���A2��B1��C2��Ȼ��д����C2�����ꣻ��3��д��B B1��A2 C1�Ľ������꼴�ɣ���4���Ȼ�������ABCD��Ȼ��д��D�����꣮
���Ӷ��õ���A2��B1��C2��Ȼ��д����C2�����ꣻ��3��д��B B1��A2 C1�Ľ������꼴�ɣ���4���Ȼ�������ABCD��Ȼ��д��D�����꣮
�⣺
��1����ͼ����A1B1C1Ϊ��������C1������Ϊ��3����1����
��2����ͼ����A2B2CΪ��������C2������Ϊ����1��3����
��3����A1BC1����A2B1C2���ڵ�![]() ���ĶԳƣ�
���ĶԳƣ�
��4����D��������4��4����
�ʴ�Ϊ��3����1��������1��3����![]() ����4��4����
����4��4����


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
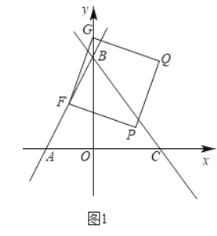
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B������B��ֱ�߽�x����C����
��x�ύ�ڵ�A����y�ύ�ڵ�B������B��ֱ�߽�x����C����![]() ���Ϊ10.
���Ϊ10.
��1�����C�����꼰ֱ��BC�Ľ���ʽ��
��2����ͼ1�����FΪ�߶�AB�е㣬��GΪy����һ���㣬����FG����FGΪ����FG�Ҳ���������FGQP����G����˶������У�������Q����ֱ��BC��ʱ�����G�����ꣻ
��3����ͼ2����MΪ�߶�BC��һ�㣬������![]() ����EΪֱ��AM��һ���㣬��x�����Ƿ���ڵ�D��ʹ�Ե�D��E��B��CΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵������.
����EΪֱ��AM��һ���㣬��x�����Ƿ���ڵ�D��ʹ�Ե�D��E��B��CΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����D�����ꣻ�������ڣ���˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���Ӫij��Ʒ�Ƶļ�����������ʱ�ĵ�����20Ԫ�������г����飺��һ��ʱ���ڣ����۵�����30Ԫʱ����������600���������۵���ÿ����1Ԫ���ͻ����۳�10����
��1�����������Ʒ�Ƽ����������۵���ΪxԪ��x��30��������ֱ���x�Ĵ���ʽ����ʾ������y�������۸�Ʒ�Ƽ������������wԪ�����ѽ����д�ڱ����У�
���۵��ۣ�Ԫ�� | x��x��30�� |
������y������ | �� �� |
���ۼ������������w��Ԫ�� | �� �� |
��2���ڵ���1���ʵ������£������������涨��Ʒ�Ƽ��������۵��۲�����35Ԫ�����̳�Ҫ��ɲ�����500���������������̳����۸�Ʒ�Ƽ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
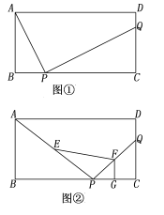
����Ŀ����֪����ͼ�٣��ڣ��ھ���ABCD�У�AB=4��BC=8��P��Q�ֱ��DZ�BC��CD�ϵĵ㣮
(1)��ͼ�٣���AP��PQ��BP=2����CQ�ij���
(2)��ͼ�ڣ���![]() =2����E��F��G�ֱ�ΪAP��PQ��PC���е㣬���ı���EPGF�������
=2����E��F��G�ֱ�ΪAP��PQ��PC���е㣬���ı���EPGF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��.
��.
��1����֤��![]() ��
��
��2����![]() ��
��![]() ����
����![]() �ij���
�ij���
��3����![]() ��
��![]() ����
����![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪m,n�Ƿ���x2��6x+5=0������ʵ��������m<n��������
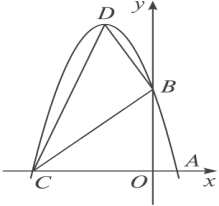
y=��x2+bx+c��ͼ����A(m,0)��B(0,n)��
(1)����������ߵĽ���ʽ��
(2)�裨1������������x�����һ����ΪC,�����ߵĶ���ΪD���������C��D���������BCD�������
(3)P���߶�OC�ϵ�һ�㣬����P��PH��x�ᣬ�������߽���H�㣬��ֱ��BC����PCH�ֳ����֮��Ϊ2��3�������֣������P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
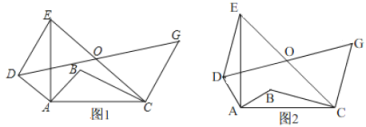
����Ŀ����ͼ���ڡ�ABC�У�AB��BC����B��90�㣬��DΪ�߶�BC��һ�����㣨�����B��C�غϣ�������AD�����߶�AD�Ƶ�D˳ʱ����ת90��õ��߶�DE������EC.
��1���������ⲹȫͼ1��
����֤����EDC����BAD;
��2����С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У��߶�CE��BD��������ϵʼ�ղ��䣬�õ�ʽ��ʾΪ�� ����
��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������E��EF��BC����BC�ӳ����ڵ�F��ֻ��֤��ADB�ա�DEF��
�뷨2�����߶�AB��ȡһ��F��ʹ��BF��BD������DF��ֻ��֤��ADF�ա�DEC��
�뷨3���ӳ�AB��F��ʹ��BF��BD������DF��CF��ֻ��֤�ı���DFCEΪƽ���ı��Σ�
����
����ο�������뷨������С��֤��(2)���еIJ��룮��һ�ַ������ɣ�
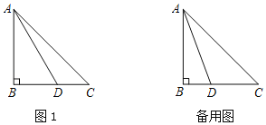
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y1��x2��2x+c�IJ���ͼ����ͼ1��ʾ��
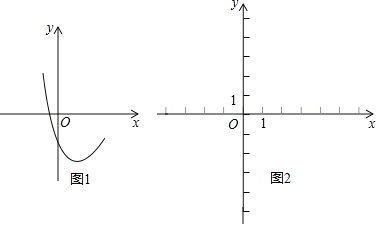
��1��ȷ��c��ȡֵ��Χ��
��2���������߾����㣨0����1������ȷ��������y1��x2��2x+c�Ľ���ʽ��
��3��������������y2��![]() ��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶ѧ��������ʵ������������������40��ͬѧʵ������ĵ÷֣����ݻ�ȡ���������ݣ����������µ�����ͳ��ͼ������ͳ��ͼ������������Ϣ������������⣺
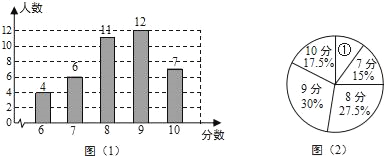
�������� �ٵ�Բ�ĽǵĴ�С���� ����
��������40���������ݵ�ƽ��������������λ����
��������У���꼶����320��ѧ�������Ƹ�У����ʵ����������֣�10�֣��ж����ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com