
����Ŀ����֪������y1��x2��2x+c�IJ���ͼ����ͼ1��ʾ��
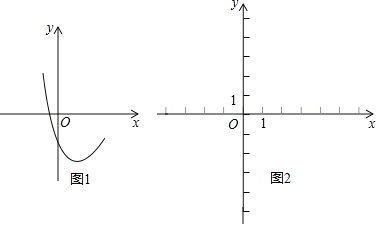
��1��ȷ��c��ȡֵ��Χ��
��2���������߾����㣨0����1������ȷ��������y1��x2��2x+c�Ľ���ʽ��
��3��������������y2��![]() ��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
���𰸡���1��c��0����2��y1��x2��2x��1����3��ͼ�����������x����1��0��x��1��x��2ʱ��y1��y2����
��������
��1������ͼ1�������ߵ�ͼ���֪��c��0����������x��Ӧ�����������㣬��ˡ���0���ɴ˿����c��ȡֵ��Χ��
��2�����㣨0����1������������������м��ɵó������Ľ���ʽ��
��3������ͼ����һ���ѵ㣬��ͼ�㼴Ϊ��ͼ������Ӧ����ʽ���ɷ�����Ľ⣬�۲�ͼ��y1��y2�����㣨1����2���⣬���������������Ϊ����1��2���ͣ�2����1������x����1��y��2��x��2��y����1�ֱ����y1��x2��2x��1��y2��![]() ��֪������1��2���ͣ�2����1����y1��y2���������㣮����ͼ���֪����x����1��0��x��1��x��2ʱ��y1��y2��
��֪������1��2���ͣ�2����1����y1��y2���������㣮����ͼ���֪����x����1��0��x��1��x��2ʱ��y1��y2��
�⣺��1������ͼ���֪c��0��
��������y1��x2��2x+c��x������������
����һԪ���η���x2��2x+c��0���������ȵ�ʵ������
���ԡ�������2��2��4c��4��4c��0����c��0
����c��0��
��2����Ϊ�����߾����㣨0����1��
��x��0��y1����1����y1��x2��2x+c
��c����1
�����������ߵĽ���ʽΪy1��x2��2x��1
��3����Ϊ����������y2��![]() ��ͼ��������y1��x2��2x��1�ϵĵ㣨1��a��
��ͼ��������y1��x2��2x��1�ϵĵ㣨1��a��
��x��1��y1��a����y1��x2��2x��1����a����2
��x��1��a����2����y2��![]() ����k����2
����k����2
����y2��![]() ��
��
����y2��![]() ��ͼ����ͼ��ʾ��
��ͼ����ͼ��ʾ��
�۲�ͼ��y1��y2�����㣨1����2���⣬���������������Ϊ����1��2���ͣ�2����1��
��x����1��y2��2��x��2��y2����1��
�ֱ����y1��x2��2x��1��y��![]() ��֪������1��2���ͣ�2����1����y1��y2����������
��֪������1��2���ͣ�2����1����y1��y2����������
����ͼ���֪����x����1��0��x��1��x��2ʱ��y1��y2��



 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB��5cm��BC��10cm����P�ӵ�A��������AB�����B��ÿ��1cm���ٶ��ƶ���ͬʱ��Q�ӵ�B������BC�����C��ÿ��2cm���ٶ��ƶ���P��Q�����ڷֱ�B��C����ʱ��ֹͣ�ƶ����������ƶ���ʱ��Ϊt�룬����������⣺
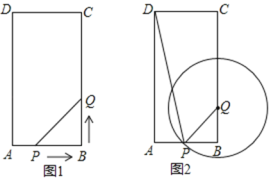
��1����ͼ1����tΪ����ʱ����PBQ���������4cm2��
��2����ͼ2����QΪԲ�ģ�PQΪ�뾶����Q�����˶������У��Ƿ����������tֵ��ʹ��Q�������ı���DPQC��һ�ߣ�������ڵ�ֱ�ߣ����У������ڣ����tֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�Ķ��������ֱ�ΪA��2��2����B��1��0����C��3��1����
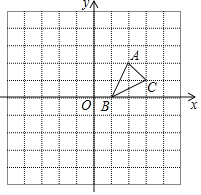
��1��������ABC����x��ԳƵ���A1BC1��д����C1������Ϊ�� ����
��2��������ABC��ԭ��O��ʱ����ת90������A2B1C2��д����C2������Ϊ�� ����
��3���ڣ�1������2���Ļ����ϣ�ͼ�е���A1BC1����A2B1C2���ڵ��� �����ĶԳƣ�
��4�����Ե�D��A��C��BΪ������ı���Ϊ���Σ�ֱ��д����D������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() ��
��![]() ������
������![]() ��.
��.
��1������![]()
![]() �����������ͼ���ϣ���
�����������ͼ���ϣ���![]() ��ֵ;
��ֵ;
��2�������������ͼ���ÿһ����֧�ϣ�![]() ��
��![]() �������������
�������������![]() ��ȡֵ��Χ;
��ȡֵ��Χ;
��3����![]() �����жϵ�
�����жϵ�![]()
![]() �Ƿ������������ͼ���ϣ���˵������.
�Ƿ������������ͼ���ϣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǡ������ǰ廭Բ�����ߡ��Ļ�ͼ������
��ͼ1����֪Բ��һ��A������A���Բ�����ߣ�
![]()

��������1����ͼ2�������ǰ��ֱ�Ƕ������Բ����һ��C�����A���غϣ�����ʹ��һֱ�DZ߾�����A����һ��ֱ�DZ���Բ����B�㣬����AB��
��2����ͼ3�������ǰ��ֱ�Ƕ������A�غϣ�ʹһ��ֱ�DZ߾�����B��������һ��ֱ�DZ����ڵ�ֱ��AD��
����ֱ��AD���ǹ���A��Բ�����ߣ�
��ش𣺸û�ͼ��������_______________________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�����ߣ�tanB=![]() ��cosC=
��cosC=![]() ��AC=
��AC=![]()
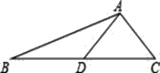
��1����BC�ij���
��2��������ABC�����Բ���߹���ͼ,�����ۼ�����д���������������Բ�뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽������ȫ�д��Ĺ���������̶ȣ�ij��ѧ��ѧ��ȤС����ȫ�мס����������ڽ����˵���ͳ�ƣ�����������Ϊ�����⣬һ�㣬���⣬�dz��������࣬���ա�������ȫ���ʾ��õ����в�������ͳ��ͼ��

����ͼ����Ϣ������������⣺
��1����˴ε����н��ܵ����������
��2����˴ε����н��Ϊ�dz������������
��3����ȤС�����ӵ�����Ϊ�������4λ���������ѡ��2λ���лطã���֪4λ��������2λ���Լ�������2λ���������������б����û���״ͼ�ķ������ѡ�����������Լ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ѵ�ڵ���֮�ʣ�ijˮ�ó��ӵ�����һ��С�ͳ�ˮ�õĽ�������Ҫ�������10���ڣ���10�죩�������Ϊ�������Ч�ʣ������Ӱ�ӵ㣬�ӵ�����ĵ�һ���������ˮ��20̨���Ժ�ÿ��������ˮ�ö���ǰһ���2 ̨�����ڻ�����ĵ�ԭ����������ˮ�������ﵽ28̨��ÿ������һ̨����������������ˮ�ã�ƽ��ÿ̨�ɱ�������20Ԫ��
��1�����![]() ������ˮ��
������ˮ��![]() ̨��ֱ��д��
̨��ֱ��д��![]() ��
��![]() ֮��ĺ�������ʽ����д���Ա���
֮��ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ÿ̨ˮ�õijɱ��ۣ���������������28̨ʱ��Ϊ1000Ԫ�����ۼ۸�Ϊÿ̨1400Ԫ�����![]() �������Ϊ
�������Ϊ![]() Ԫ������
Ԫ������![]() ��
��![]() ֮��ĺ�������ʽ������ó���һ���õ�������������������٣�
֮��ĺ�������ʽ������ó���һ���õ�������������������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AC��BC����ACB��90������P����ƽ���ڲ����A��B��C�غϵ�����һ�㣬����PC�����߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC������AD��BP��
��1���۲����
����P��ֱ��AC��ʱ����ͼ1���߶�BP��AD��������ϵ���� ����ֱ��BP��ֱ��AD��λ�ù�ϵ���� ����
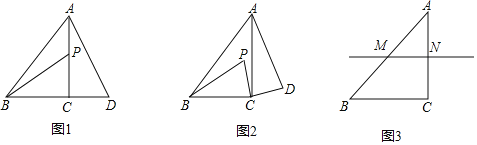
��2����չ̽��
����P����ֱ��AC��ʱ����1���е�������ϵ��λ�ù�ϵ�������𣿲���ͼ2������˵�����ɣ�
��3���������
����M��N�ֱ���AB��AC���е㣬��P��ֱ��MN�ϣ���ֱ��д����A��P��D��ͬһ��ֱ����ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com