
【题目】如图,AD是△ABC的中线,tanB=![]() ,cosC=
,cosC=![]() ,AC=
,AC=![]()
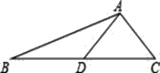
(1)求BC的长;
(2)作出△ABC的外接圆(尺规作图,保留痕迹,不写作法),并求外接圆半径.
【答案】(1)5;(2)AO=![]() .
.
【解析】
(1)过点A作AE⊥BC于点E,根据三角函数的定义和特殊角的三角函数即可得出.
(2)作AB、AC的垂直平分线,交点O即为圆心,以0A为半径作圆,即可得出△ABC的外接圆,根据sin∠ABC=sin∠AOK即可求解.
解:(1)如图过点A作AE⊥BC于点E,

∵cosC=![]() ,
,
∴∠C=45°,
在Rt△ACE中,CE=ACcosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=![]() ,即
,即![]() ,
,
∴BE=4AE=4,
∴BC=BE+CE=5.
(2)如图,⊙O就是所求作的△ABC的外接圆.

∵∠AOC=2∠ABC,∠AOK=∠COK,∴∠ABC=∠AOK,
∵sin∠AOK=sin∠ABC=![]()
由(1)可知AB=![]()
∴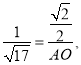
∴AO=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且![]() .
.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若![]() 的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
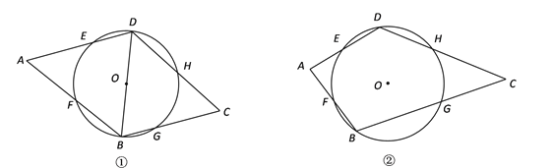
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线
y=-x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
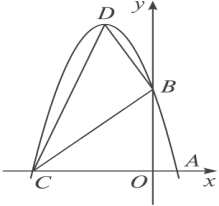
查看答案和解析>>
科目:初中数学 来源: 题型:
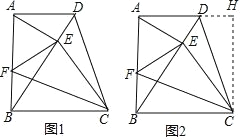
【题目】已知:如图,四边形 ABCD 中,AD∥BC,∠ABC=90°,AB=BC,AE⊥BD,EF⊥CE
(1)试证明△AEF∽△BEC;
(2)如图,过 C 点作 CH⊥AD 于 H,试探究线段 DH 与 BF 的数量关系,并说明理由;
(3)若 AD=1,CD=5,试求出 BE 的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=x2﹣2x+c的部分图象如图1所示:
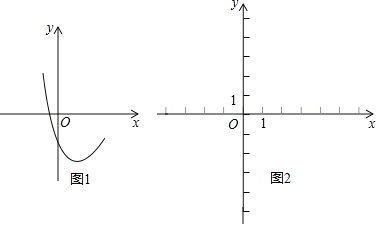
(1)确定c的取值范围;
(2)若抛物线经过点(0,﹣1),试确定抛物线y1=x2﹣2x+c的解析式;
(3)若反比例函数y2=![]() 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象写出当y1>y2时,对应自变量x的取值范围.
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象写出当y1>y2时,对应自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )
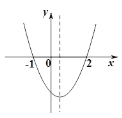
A.函数有最小值B.图象对称轴是直线x=![]()
C.当x<![]() ,y随x的增大而减小D.当-1<x<2时,y>0
,y随x的增大而减小D.当-1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
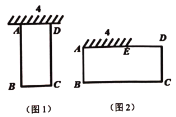
【题目】如图,校园空地上有一面墙,长度为4米,为了创建“美丽校园”,学校决定借用这面墙和20米的围栏围成一个矩形花园![]() ,设
,设![]() 长为
长为![]() 米,矩形花园
米,矩形花园![]() 的面积为
的面积为![]() 平方米.
平方米.
(1)如图1,若所围成的矩形花园![]() 边的长不得超出这面墙,求
边的长不得超出这面墙,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,当![]() 为何值时,矩形花园
为何值时,矩形花园![]() 的面积最大,最大值是多少?
的面积最大,最大值是多少?
(3)如图2,若围成的矩形花园![]() 的
的![]() 边的长可超出这面墙,求围成的矩形
边的长可超出这面墙,求围成的矩形![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车逐渐成为市民喜爱的“绿色出行” 方式之一,今年国庆假期某一天,济川中学初三数学社团的同学们随机调查了一个社区,将这天部分出行市民使用共享单车的数据整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 这天部分出行市民使用共享单车次数的中位数是__________,众数是__________
(2) 这天部分出行市民平均每人使用共享单车多少次?
(3) 若该社区这天有1500人出行,请你估计这天使用共享单车次数在3次以上(含3 次)的市民有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com