
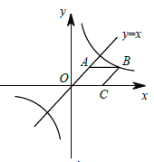
【题目】如图,已知菱形![]() ,点
,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 经过点
经过点![]() ,菱形
,菱形![]() 的面积是
的面积是![]() . 若反比例函数
. 若反比例函数![]() 的图象经过点
的图象经过点![]() ,则此反比例函数表达式中的
,则此反比例函数表达式中的![]() 为_____.
为_____.
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,tanB=![]() ,cosC=
,cosC=![]() ,AC=
,AC=![]()
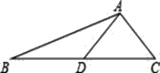
(1)求BC的长;
(2)作出△ABC的外接圆(尺规作图,保留痕迹,不写作法),并求外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“特色泰兴,美好生活”, 泰兴举行金色秋天旅游活动.明明和华华同学分析网上关于旅游活动的信息,发现最具特色的景点有:①小南湖、②古银杏公园、③红枫园.他们准备周日下午去参观游览,各自在这三中个景点任选一个,每个景点被选中的可能性相同.
(1)明明同学在三个备选景点中选中小南湖的概率是_____.
(2)用树状图或列表法求出明明和华华他们选中不同景点参观的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,点E是BC上的一个动点,将△CDE绕着点E逆时针旋转90°,得到△C′D′E,则A,D′两点距离的最小值等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°.点P在是平面内不与点A,B,C重合的任意一点,连接PC,将线段PC绕点C顺时针旋转90°得到线段DC,连接AD,BP.
(1)观察猜想
当点P在直线AC上时,如图1,线段BP与AD的数量关系是 ,直线BP与直线AD的位置关系是 ;
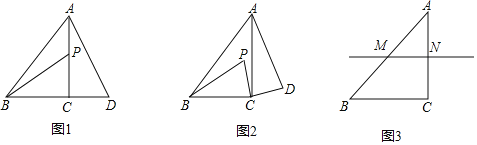
(2)拓展探究
当点P不在直线AC上时,(1)中的数量关系和位置关系还成立吗?并就图2的情形说明理由;
(3)解决问题
若点M,N分别是AB和AC的中点,点P在直线MN上,请直接写出点A,P,D在同一条直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与原点重合,
与原点重合,![]() 、
、![]() 分别在坐标轴上,
分别在坐标轴上,![]() ,
,![]() ,直线
,直线![]() 交
交![]() ,
,![]() 分别于点
分别于点![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,
,![]() .
.
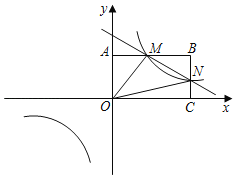
(1)求反比例函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 的面积与四边形
的面积与四边形![]() 的面积相等,求点
的面积相等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD的两边AB、BC的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)试说明:无论m取何值方程总有两个实数根
(2)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(3)若AB的长为2,那么平行四边形ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,以点![]() (3,0)为圆心,以6为半径的圆分别交
(3,0)为圆心,以6为半径的圆分别交![]() 轴的正半轴于点
轴的正半轴于点![]() ,交
,交![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 轴的负半轴于点
轴的负半轴于点![]() (-9,0)
(-9,0)
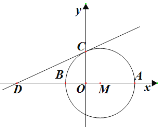
(1)求![]() 两点的坐标;
两点的坐标;
(2)若抛物线![]() 经过
经过![]() 、
、![]() 两点,求此抛物线的解析式;
两点,求此抛物线的解析式;
(3)求证:直线![]() 是⊙
是⊙![]() 的切线;
的切线;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,恰好选中《九章算术》和《孙子算经》的概率是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com