
【题目】如图,在正方形ABCD中,AB=4,点E是BC上的一个动点,将△CDE绕着点E逆时针旋转90°,得到△C′D′E,则A,D′两点距离的最小值等于_____.

【答案】2![]()
【解析】
C′D′交AB于F,如图,设CE=x,则BE=4-x,利用旋转的性质得到EC′=EC=x,C′D′=CD=4,∠EC′D′=∠C=90°,则C′D′⊥AB,利用四边形BFC′E为矩形得到C′F=BE=4-x,BF=EC′=x,所以FD′=x,AF=4-x,根据勾股定理得到AD′=![]() ,然后利用非负数的性质可确定AD′的最小值.
,然后利用非负数的性质可确定AD′的最小值.
解:C′D′交AB于F,如图,
设CE=x,则BE=4﹣x,
∵△CDE绕着点E逆时针旋转90°,得到△C′D′E,
∴EC′=EC=x,C′D′=CD=4,∠EC′D′=∠C=90°,
∴C′D′⊥AB,
易得四边形BFC′E为矩形,
∴C′F=BE=4﹣x,BF=EC′=x,
∴FD′=x,AF=4﹣x,
在Rt△AFD′中,AD′=![]() ,
,
∵2(x﹣2)2≥0,
∴AD′的最小值为![]() .
.
故答案为![]() .
.



 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
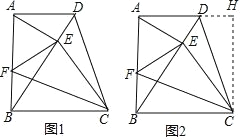
【题目】已知:如图,四边形 ABCD 中,AD∥BC,∠ABC=90°,AB=BC,AE⊥BD,EF⊥CE
(1)试证明△AEF∽△BEC;
(2)如图,过 C 点作 CH⊥AD 于 H,试探究线段 DH 与 BF 的数量关系,并说明理由;
(3)若 AD=1,CD=5,试求出 BE 的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车逐渐成为市民喜爱的“绿色出行” 方式之一,今年国庆假期某一天,济川中学初三数学社团的同学们随机调查了一个社区,将这天部分出行市民使用共享单车的数据整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 这天部分出行市民使用共享单车次数的中位数是__________,众数是__________
(2) 这天部分出行市民平均每人使用共享单车多少次?
(3) 若该社区这天有1500人出行,请你估计这天使用共享单车次数在3次以上(含3 次)的市民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
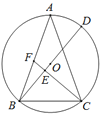
【题目】如图,△ABC内接于⊙O,AB=AC,CF垂直直径BD于点E,交边AB于点F.
(1)求证:∠BFC=∠ABC.
(2)若⊙O的半径为5,CF=6,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,直线 y=kx+b 分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).
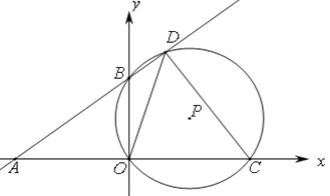
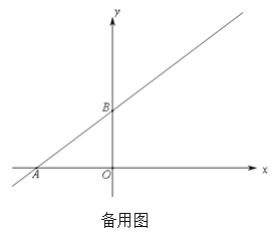
(1)求直线AB的函数表达式.
(2)若点D在第一象限,且tan∠ODC=![]() , 求点D的坐标.
, 求点D的坐标.
(3)当△ODC为等腰三角形时,求出所有符合条件的m的值.
(4)点P,Q关于OD成轴对称,当点Q恰好落在直线AB上时,直接写出此时BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
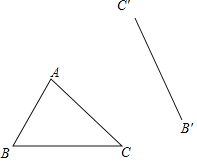
【题目】如图,求作△ABC绕某点旋转一定角度后的△A′B′C′时,某同学只作了一部分图形.
(1)请把△A′B′C′作完整,并保留作图痕迹;
(2)写出基本作图步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为![]() ,则由题意列方程应为____________________________ 。
,则由题意列方程应为____________________________ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com