
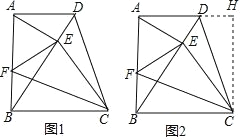
【题目】已知:如图,四边形 ABCD 中,AD∥BC,∠ABC=90°,AB=BC,AE⊥BD,EF⊥CE
(1)试证明△AEF∽△BEC;
(2)如图,过 C 点作 CH⊥AD 于 H,试探究线段 DH 与 BF 的数量关系,并说明理由;
(3)若 AD=1,CD=5,试求出 BE 的值?
【答案】(1)证明见解析;(2)DH=BF,理由见解析;(3)BE=![]() .
.
【解析】
(1)想办法证明∠AEF=∠BEC,∠FAE=∠EBC即可解决问题;
(2)结论:DH=BF.利用比例的性质首先证明AD=AF,再证明四边形ABCH是正方形即可解决问题;
(3)设正方形的边长为x,在Rt△CDH中,DH=x-1,CH=x,CD=5,可得52=x2+(x-1)2,解得x=4,再通过解直角三角形求出BE的长即可.
(1)证明:∵AE⊥BD,EF⊥CE,
∴∠AEB=∠FEC=90°,
∴∠AEF=∠BEC,
∵∠ABC=90°,
∴∠ABE+∠EBC=90°,∠ABE+∠FAE=90°,
∴∠FAE=∠EBC,
∴△AEF∽△BEC;
(2)解:结论:DH=BF.
理由:∵△AEF∽△BEC,
∴![]() ,
,
∵∠ABE=∠ABD,∠AEB=∠BAD=90°,
∴△ABE∽△DBA,
∴![]() ,
,
∴![]() ,∵BC=AB,
,∵BC=AB,
∴AF=AD,
∵∠ABC=∠BAD=∠H=90°,
∴四边形ABCH是矩形,
∵AB=BC,
∴四边形ABCH是正方形,
∴AB=AH,∵AF=AD,
∴BF=DH.
(3)设正方形的边长为x,
在Rt△CDH中,DH=x-1,CH=x,CD=5,
∴52=x2+(x-1)2,
解得x=4,
∴AB=4,AD=1,
在Rt△ABD中,BD=![]() ,
,
∵![]() ADAB=
ADAB=![]() BDAE,
BDAE,
∴AE=![]() ,
,
在Rt△AEB中,BE=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
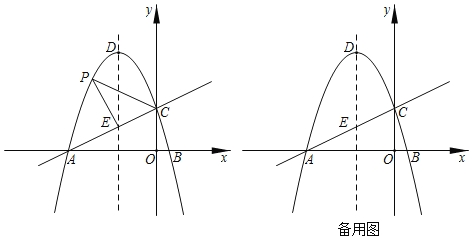
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x+
x+![]() 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,抛物线的对称轴与直线AC交于点E.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,抛物线的对称轴与直线AC交于点E.
(1)若点P为直线AC上方抛物线上的动点,连接PC,PE,当△PCE的面积S△PCE最大时,点P关于抛物线对称轴的对称点为点Q,此时点T从点Q开始出发,沿适当的路径运动至y轴上的点F处,再沿适当的路径运动至x轴上的点G处,最后沿适当的路径运动至直线AC上的点H处,求满足条件的点P的坐标及QF+FG+![]() AH的最小值.
AH的最小值.
(2)将△BOC绕点B顺时针旋转120°,边BO所在直线与直线AC交于点M,将抛物线沿射线CA方向平移![]() 个单位后,顶点D的对应点为D′,点R在y轴上,点N在坐标平面内,当以点D′,R,M,N为顶点的四边形是菱形时,请直接写出N点坐标.
个单位后,顶点D的对应点为D′,点R在y轴上,点N在坐标平面内,当以点D′,R,M,N为顶点的四边形是菱形时,请直接写出N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() .
.

(1)画出![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后的图形
后的图形![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)将(1)中所得![]() 先向左平移4个单位,再向上平移2个单位得到
先向左平移4个单位,再向上平移2个单位得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(3)若![]() 可以看作
可以看作![]() 绕某点旋转得来,直接写出旋转中心的坐标.
绕某点旋转得来,直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知反比例函数![]() (
(![]() 常数,
常数,![]() ).
).
(1)若点![]()
![]() 在这个函数的图象上,求
在这个函数的图象上,求![]() 的值;
的值;
(2)若在这个函数图象的每一个分支上,![]() 随
随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
(3)若![]() ,试判断点
,试判断点![]()
![]() 是否在这个函数的图象上,并说明理由.
是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
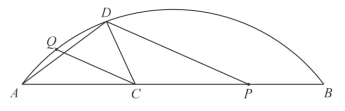
【题目】如图,Q是![]() 上一定点,P是弦AB上一动点,C为AP中点,连接CQ,过点P作
上一定点,P是弦AB上一动点,C为AP中点,连接CQ,过点P作![]() 交
交![]() 于点D,连接AD,CD.
于点D,连接AD,CD.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,C,D两点间的距离为
,C,D两点间的距离为![]() .
.
(当点P与点A重合时,令y的值为1.30)
小荣根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探宄.
下面是小荣的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:

(2)建立平面直角坐标系,描出以补全后的表中各组对应值为坐标的点,画出该函数的图象;

(3)结合函数图象,解决问题:当![]() 时,AP的长度约为__________cm.
时,AP的长度约为__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,tanB=![]() ,cosC=
,cosC=![]() ,AC=
,AC=![]()
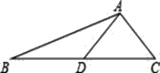
(1)求BC的长;
(2)作出△ABC的外接圆(尺规作图,保留痕迹,不写作法),并求外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
(1)求这条抛物线的解析式;
(2)画出此抛物线;
(3)若抛物线与![]() 轴的另一个交点为E,求△ODE的面积;
轴的另一个交点为E,求△ODE的面积;
(4)抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出点P的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,点E是BC上的一个动点,将△CDE绕着点E逆时针旋转90°,得到△C′D′E,则A,D′两点距离的最小值等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com