
����Ŀ������ABC�У�AC��BC����ACB��90������P����ƽ���ڲ����A��B��C�غϵ�����һ�㣬����PC�����߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC������AD��BP��
��1���۲����
����P��ֱ��AC��ʱ����ͼ1���߶�BP��AD��������ϵ���� ����ֱ��BP��ֱ��AD��λ�ù�ϵ���� ����
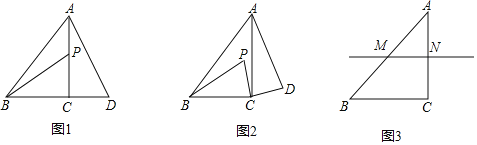
��2����չ̽��
����P����ֱ��AC��ʱ����1���е�������ϵ��λ�ù�ϵ�������𣿲���ͼ2������˵�����ɣ�
��3���������
����M��N�ֱ���AB��AC���е㣬��P��ֱ��MN�ϣ���ֱ��д����A��P��D��ͬһ��ֱ����ʱ![]() ��ֵ��
��ֵ��
���𰸡���1��BP��AD��BP��AD����2�����������ɼ���������3��![]() ��
�� ![]()
��������
��1���۲����,��ͼ1���ӳ�BP��AD��H������SAS����֤��ACD�ա�BCP���ɵ�BP=AD����CAD=��CBP������ǵ����ʿ�֤BP��AD��
��2����չ̽��,��ͼ2���ӳ�BP��AD��H������SAS����֤��ACD�ա�BCP���ɵ�BP=AD����CAD=��CBP�����������ڽǺͶ�����֤BP��AD��
��3���������,������������ۣ�����SAS����֤��ACD�ա�BCP���ɵ�BP=AD�����߶δ�ֱƽ���ߵ����ʿɵ�AP=PC��������⣮
�⣺��1���۲����
��ͼ1���ӳ�BP��AD��H��

�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90����
���ACB����PCD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��BP��AD����CAD����CBP��
�ߡ�CAD+��D��90����
���CBP+��D��90����
���BHD��90����
��BP��AD��
�ʴ�Ϊ��BP��AD��BP��AD��
��2����չ̽��
��Ȼ������
�������£���ͼ2���ӳ�BP��AD��H��
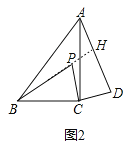
�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90������ACB��
���BCP����ACD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��BP��AD����CAD����CBP��
�ߡ�CBP+��ABP+��BAC��90����
���CAD+��ABP+��BAC��90����
���AHB��90����
��BP��AD��
��3���������
����A���߶�PD��ʱ����ͼ3������BP��
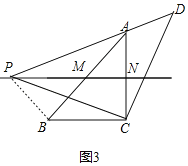
�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90������ACB��
���BCP����ACD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��PB��AD��
�ߵ�M��N�ֱ���AB��AC���е㣬
��MN��BC��
���ANM����ACB��90������AN��CN��
��PN��AC���д��ߣ�
��AP��PC��
��PC��CD����PCD��90��
��PD��![]() PC��
PC��
��AD��PD��AP��![]() PC��PC��BP��
PC��PC��BP��
��![]() ��
��
����P���߶�AD��ʱ����ͼ4������BP��

�߽��߶�PC�Ƶ�C˳ʱ����ת90���õ��߶�DC��
��PC��CD����PCD��90������ACB��
���BCP����ACD��90������AC��BC��PC��CD��
���ACD�ա�BCP��SAS��
��PB��AD��
�ߵ�M��N�ֱ���AB��AC���е㣬
��MN��BC��
���ANM����ACB��90������AN��CN��
��PN��AC���д��ߣ�
��AP��PC��
��PC��CD����PCD��90��
��PD��![]() PC��
PC��
��AD��PD+AP��![]() PC+PC��BP��
PC+PC��BP��
��![]() ��
��


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y1��x2��2x+c�IJ���ͼ����ͼ1��ʾ��
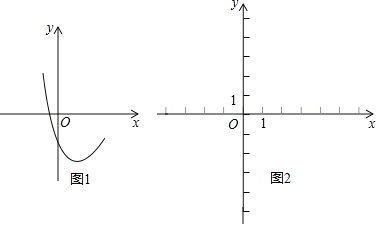
��1��ȷ��c��ȡֵ��Χ��
��2���������߾����㣨0����1������ȷ��������y1��x2��2x+c�Ľ���ʽ��
��3��������������y2��![]() ��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
��ͼ����2�����������ϵ㣨1��a��������ͼ2��ʾֱ������ϵ�У������÷�������������2���������ߵ�ͼ������ͼ��д����y1��y2ʱ����Ӧ�Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ���꼶ѧ��������ʵ������������������40��ͬѧʵ������ĵ÷֣����ݻ�ȡ���������ݣ����������µ�����ͳ��ͼ������ͳ��ͼ������������Ϣ������������⣺
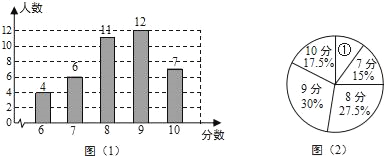
�������� �ٵ�Բ�ĽǵĴ�С���� ����
��������40���������ݵ�ƽ��������������λ����
��������У���꼶����320��ѧ�������Ƹ�У����ʵ����������֣�10�֣��ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У�ֱ�� y=kx+b �ֱ�x,y���ڵ�A(-8��0)��B(0��6)��C��m,0��������AO��һ���㣬��P��B��O��C���㣬��ֱ��AB�ڵ�D��B��D���غϣ�.
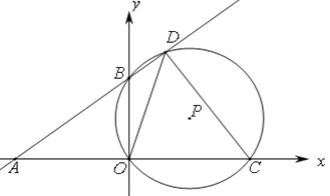
��1����ֱ��AB�ĺ�������ʽ.
��2������D�ڵ�һ���ޣ���tan��ODC=![]() �� ���D������.
�� ���D������.
��3������ODCΪ����������ʱ��������з���������m��ֵ.
��4����P��Q����OD����Գƣ�����Qǡ������ֱ��AB��ʱ��ֱ��д����ʱBQ�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����2a��1��x+a2+2��0����������ȵ�ʵ������
��1����ʵ��a��ȡֵ��Χ������a�����������
��2��x��1�����Ƿ��̵�һ���������ǣ������������һ�����������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
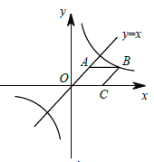
����Ŀ����ͼ����֪����![]() ����
����![]() ��
��![]() ���ϣ�ֱ��
���ϣ�ֱ��![]() ������
������![]() ������
������![]() �������
�������![]() . ������������
. ������������![]() ��ͼ����
��ͼ����![]() ����˷�������������ʽ�е�
����˷�������������ʽ�е�![]() Ϊ_____.
Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ��
��![]() �����˶����ٶȾ�Ϊ
�����˶����ٶȾ�Ϊ![]() ;���˶�������ʼ�ձ���
;���˶�������ʼ�ձ���![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() . ����
. ����![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() .
.
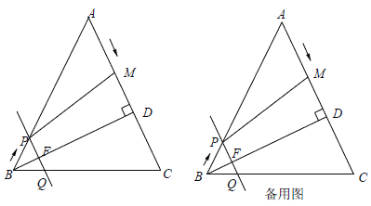
��1����![]() _____ʱ���ı���
_____ʱ���ı���![]() ��ƽ���ı���.
��ƽ���ı���.
��2������![]() ��
��![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ;�������ڣ�˵�����ɣ�
��ֵ;�������ڣ�˵�����ɣ�
��4������![]() ���Ƿ����ijһʱ��
���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() ���߶�
���߶�![]() �Ĵ�ֱƽ�����ϣ������ڣ���ֱ��д����ʱ
�Ĵ�ֱƽ�����ϣ������ڣ���ֱ��д����ʱ![]() ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣�ijУ�ڻ��زμ����ʵ�������У�������ʦ����ѧ�������ؼƻ��½�һ�����ε������أ�һ�߿���ǽ��ǽ�㹻�����������������ܳ�69�IJ����դ��Χ�ɣ���ǽƽ�е�һ����һ����Ϊ3�ij���ڣ���ͼ��ʾ�������Ʋ���ʹ�صĶ��������������λѧ��������龳��
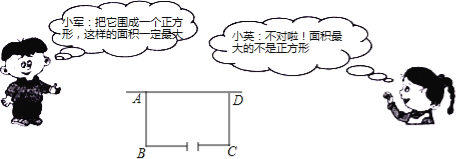
������������Ϣ��������⣺
��1����AB=x�ף�x��0�������ú�x�Ĵ���ʽ��ʾBC�ij���
��2�������ж�˭��˵����ȷ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ4��������ֽƬABCD�۵���ʹ�õ�A���ڱ�CD���е�E�����ۺ�ΪFG����F��G�ֱ��ڱ�AD��BC�ϣ����ۺ�FG�ij���Ϊ_____.
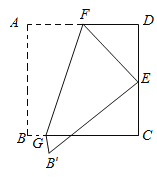
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com