
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,且
,且![]() ,点
,点![]() 分别从点
分别从点![]() 向
向![]() 向
向![]() 匀速运动,速度均为
匀速运动,速度均为![]() ;且运动过程中始终保持
;且运动过程中始终保持![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() . 连接
. 连接![]() ,设运动时间为
,设运动时间为![]() .
.
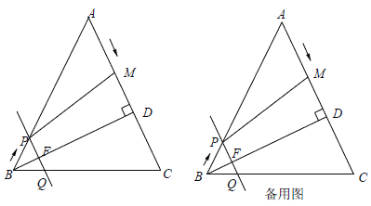
(1)当![]() _____时,四边形
_____时,四边形![]() 是平行四边形.
是平行四边形.
(2)连接![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(4)连接![]() ,是否存在某一时刻
,是否存在某一时刻![]() ,使点
,使点![]() 在线段
在线段![]() 的垂直平分线上?若存在,请直接写出此时
的垂直平分线上?若存在,请直接写出此时![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)2. 5;(2)![]() ;(3)
;(3)![]() ;(4)存在,
;(4)存在,![]()
【解析】
(1)假设PQCM为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
(2)根据PQ∥AC可得△PBQ∽△ABC,根据相似三角形的形状必然相同可知△BPQ也为等腰三角形,即BP=PQ=t,再由证得的相似三角形得底比底等于高比高,用含t的代数式就可以表示出BF,进而得到三角形的高![]() ,又点M的运动速度和时间可知点M走过的路程AM=t,所以三角形的底CM=5-t.最后根据三角形的面积公式即可得到y与t的关系式;
,又点M的运动速度和时间可知点M走过的路程AM=t,所以三角形的底CM=5-t.最后根据三角形的面积公式即可得到y与t的关系式;
(3)根据三角形的面积公式,先求出三角形ABC的面积,又根据第二问求出的y与t的解析式中列比例式求出t的值即可;
(4)假设存在,则根据垂直平分线上的点到线段两端点的距离相等即可得到MP=MC,过点M作MH垂直AB,由一对公共角的相等和一对直角的相等即可得到△AHM∽△ADB,由相似得到对应边成比例进而用含t的代数式表示出AH和HM的长,再由AP的长减AH的长表示出PH的长,从而在直角三角形PHM中根据勾股定理表示出MP的平方,再由AC的长减AM的长表示出MC的平方,根据两者的相等列出关于t的方程进而求出t的值.
(1)假设四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即5-t=t,
解得:t=2.5,
∴当t=2.5时,四边形PQCM是平行四边形;
(2)∵PQ∥AC,AB=AC
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴![]() ,即
,即![]() ,解得:BF=
,解得:BF=![]() ,
,
∴FD=BD-BF=4-![]() ,
,
又∵MC=AC-AM=5-t,
∴y=![]() MCFD=
MCFD=![]() (5-t)(4-
(5-t)(4-![]() )
)
即![]() ;
;
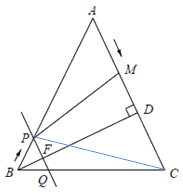
(3)存在;
∵S△ABC=![]() ACBD=
ACBD=![]() ×5×4=10,
×5×4=10,
![]() ,
,
根据题意可得:
解得:t=2,或t=8,
∵8>5,所以t=8不合题意,舍去
∴t=2;
(4)假设存在某一时刻t,使得M在线段PC的垂直平分线上,则MP=MC,
过M作MH⊥AB,交AB与H,如图所示:
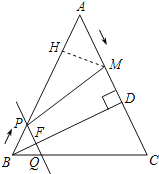
∵∠A=∠A,∠AHM=∠ADB=90°,
∴△AHM∽△ADB,
∴![]() ,
,
又∵AD=![]()
∴![]() ,
,
∴HM=![]() ,AH=
,AH=![]() ,
,
∴HP=5-t-![]() =5-
=5-![]() ,
,
在Rt△HMP中,MP2=(![]() )2+(5-
)2+(5-![]() )2=
)2=![]() t2-16t+25,
t2-16t+25,
又∵MC2=(5-t)2=25-10t+t2,
∵MP2=MC2,
∴![]() t2-16t+25=25-10t+t2
t2-16t+25=25-10t+t2
得t1=![]() ,t2=0(舍去),
,t2=0(舍去),
∴t=![]() s时,点M在线段PC的垂直平分线上.
s时,点M在线段PC的垂直平分线上.


科目:初中数学 来源: 题型:
【题目】为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.

请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
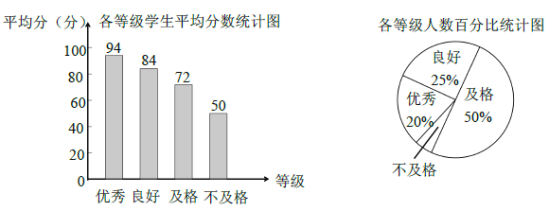
【题目】《中学生体质健康标准》规定学生体质健康等级标准为:90分及以上为优秀;80分~89分为良好;60分~79分为及格;59分及以下为不及格. 某校从九年级学生中随机抽取了![]() 的学生进行了体质测试,得分情况如下图.
的学生进行了体质测试,得分情况如下图.
(1)在抽取的学生中不及格人数所占的百分比是 ,它的圆心角度数为 度.
(2)小明按以下方法计算出抽取的学生平均得分是:![]() . 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
. 根据所学的统计知识判断小明的计算是否正确,若不正确,请计算正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°.点P在是平面内不与点A,B,C重合的任意一点,连接PC,将线段PC绕点C顺时针旋转90°得到线段DC,连接AD,BP.
(1)观察猜想
当点P在直线AC上时,如图1,线段BP与AD的数量关系是 ,直线BP与直线AD的位置关系是 ;
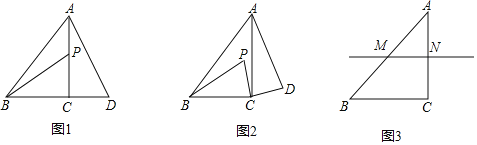
(2)拓展探究
当点P不在直线AC上时,(1)中的数量关系和位置关系还成立吗?并就图2的情形说明理由;
(3)解决问题
若点M,N分别是AB和AC的中点,点P在直线MN上,请直接写出点A,P,D在同一条直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD的两边AB、BC的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)试说明:无论m取何值方程总有两个实数根
(2)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(3)若AB的长为2,那么平行四边形ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C逆时针旋转α,(0°<α≤60°),得到△DEC,设直线DE与直线AB相交于点P.
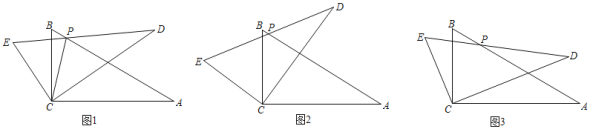
(1)如图1,连接PC,求证:PC平分∠EPA.
(2)如图2,在△ABC旋转过程中,连接BE,当△BCE的面积为9![]() 时,求α的度数.
时,求α的度数.
(3)如图3,当点P在边AB上时,问:PE+PB是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,将小旗ACDB放于平面直角坐标系中,得到各顶点的坐标为A(﹣6,12),B(﹣6,0),C(0,6),D(﹣6,6).以点B为旋转中心,在平面直角坐标系内将小旗顺时针旋转90°.

(1)画出旋转后的小旗A′C′D′B′;
(2)写出点A′,C′,D′的坐标;
(3)求出线段BA旋转到B′A′时所扫过的扇形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com