
【题目】已知Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C逆时针旋转α,(0°<α≤60°),得到△DEC,设直线DE与直线AB相交于点P.
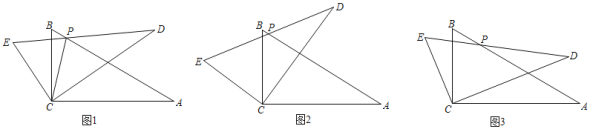
(1)如图1,连接PC,求证:PC平分∠EPA.
(2)如图2,在△ABC旋转过程中,连接BE,当△BCE的面积为9![]() 时,求α的度数.
时,求α的度数.
(3)如图3,当点P在边AB上时,问:PE+PB是否为定值?如果是,请求出此定值;如果不是,请说明理由.
【答案】(1)见解析;(2)α=60°;(3)PB+PE=6.
【解析】
(1)过C点作CN⊥DE于N,CF⊥AB于F,根据旋转前后三角形的面积不变作为相等关系得到CF=CN,从而判定PC平分∠EPA.
(2)如图2中,作EN⊥BC于N.利用三角形的面积公式构建方程求出sinα的值即可解决问题.
(3)如图3中,在PA上截取PM=PE连接CM,过C作CK⊥PA,CH⊥DE于H,连接PC.证明△PMC≌△PEC(SAS),CE=CM,PE=PM,推出PB+PE=BM,求出BM即可解决问题.
(1)过C点作CN⊥DE于N,CF⊥AB于F.
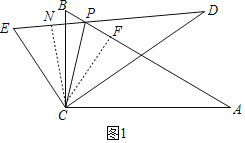
∵△ABC≌△DEC,
∴AB=DE.
∵S△ABC=![]() ABCF=S△DCE=
ABCF=S△DCE=![]() DECN,
DECN,
∵CF=CN,
∴PC平分∠EPA.
(2)如图2中,作EN⊥BC于N.
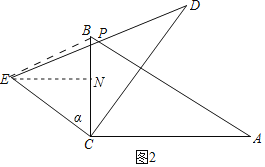
∵△BCE的面积为9![]() ,BC=EC=6,
,BC=EC=6,
∴![]() BCEN=9
BCEN=9![]() ,
,
∴![]() BCECsinα=9
BCECsinα=9![]() ,
,
∴sinα=![]() ,
,
∴α=60°.
(3)如图3中,在PA上截取PM=PE连接CM,过C作CK⊥PA,CH⊥DE于H,连接PC.
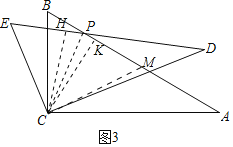
由(1)同理可证CP平分∠EPA,
∴∠EPC=∠APC,
∵PM=PE,PC=PC,
∴△PMC≌△PEC(SAS),
∴CE=CM,PE=PM.
又∵CE=CB,
∴CM=CB=6,且CK⊥PA,
∴K为BM的中点,即BK=![]() BM,
BM,
在Rt△BCK中,BK=BCcos60=6×![]() =3,
=3,
∴KM=BK=6,
∴PB+PE=PB+PM=BM=6.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2a﹣1)x+a2+2=0有两个不相等的实数根.
(1)求实数a的取值范围,并求a的最大整数;
(2)x=1可能是方程的一个根吗?若是,请求出它的另一个根,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,且
,且![]() ,点
,点![]() 分别从点
分别从点![]() 向
向![]() 向
向![]() 匀速运动,速度均为
匀速运动,速度均为![]() ;且运动过程中始终保持
;且运动过程中始终保持![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() . 连接
. 连接![]() ,设运动时间为
,设运动时间为![]() .
.
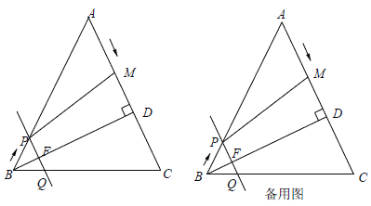
(1)当![]() _____时,四边形
_____时,四边形![]() 是平行四边形.
是平行四边形.
(2)连接![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(4)连接![]() ,是否存在某一时刻
,是否存在某一时刻![]() ,使点
,使点![]() 在线段
在线段![]() 的垂直平分线上?若存在,请直接写出此时
的垂直平分线上?若存在,请直接写出此时![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
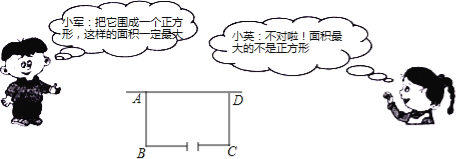
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
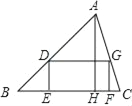
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
(1)求证:AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
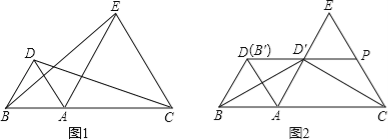
(1)连结BE,CD,求证:BE=CD;
(2)如图2,将△ABD绕点A顺时针旋转得到△AB′D′.
①当旋转角为 度时,边AD′落在AE上;
②在①的条件下,延长DD’交CE于点P,连接BD′,CD′.当线段AB、AC满足什么数量关系时,△BDD′与△CPD′全等?并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=ax2+bx+a-5(a、b为常数,a≠0),且2a+b=3.
(1)若该二次函数的图象经过点(-1,4),求该二次函数的解析式.
(2)无论a取何常数,这个二次函数的图象始终经过一个定点,求出这个定点坐标.
(3)已知点P(x0,m)和Q(1,n)都在二次函数的图象上,若x0<1,且m>n,求x0的取值范围(用含a的代数式表示)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com