
【题目】设二次函数y=ax2+bx+a-5(a、b为常数,a≠0),且2a+b=3.
(1)若该二次函数的图象经过点(-1,4),求该二次函数的解析式.
(2)无论a取何常数,这个二次函数的图象始终经过一个定点,求出这个定点坐标.
(3)已知点P(x0,m)和Q(1,n)都在二次函数的图象上,若x0<1,且m>n,求x0的取值范围(用含a的代数式表示)。
【答案】(1)y=3x2-3x-2;(2)(1,-2);(3)![]() (a>0)
(a>0)
【解析】
(1)将点(-1,4),即可求该二次函数的表达式
(2)将2a+b=3代入二次函数y=ax2+bx+a-5(a,b为常数,a≠0)中,整理得y=[ax2+(3-2a)x+a-3]-2=(ax-a+3)(x-1)-2,可知恒过点(1,2);
(3)通过y=ax2+(3-2a)x+a-5,可求得对称轴为 ![]() ,因为x0<1,且m>n,所以只需判断对称轴的位置即可求x0的取值范围.
,因为x0<1,且m>n,所以只需判断对称轴的位置即可求x0的取值范围.
解:(1)∵函数y=ax2+bx+a-5的图象经过点(-1,4),且2a+b=3,
![]()
![]()
∴二次函数的解析式为y=3x2-3x-2;
(2)∵2a+b=3,
∴二次函数y=ax2+bx+a-5=ax2+(3-2a)x+a-5,
整理得,y=[ax2+(3-2a)x+a-3]-2=(ax-a+3)(x-1)-2
∴当x=1时,y=-2,
∴这个二次函数的图象始终经过一个定点,这个定点坐标为(1,-2);
(3)∵y=ax2+(3-2a)x+a-5,
∴对称轴为![]()
∵x0<1,且m>n,
∴当a>0时,对称轴![]()
解得:![]()
当a<0时,对称轴![]()
解得:![]() (不符合题意,故x0不存在)
(不符合题意,故x0不存在)
故x0的取值范围为:![]()


科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C逆时针旋转α,(0°<α≤60°),得到△DEC,设直线DE与直线AB相交于点P.
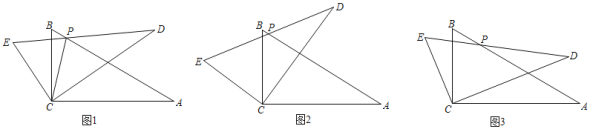
(1)如图1,连接PC,求证:PC平分∠EPA.
(2)如图2,在△ABC旋转过程中,连接BE,当△BCE的面积为9![]() 时,求α的度数.
时,求α的度数.
(3)如图3,当点P在边AB上时,问:PE+PB是否为定值?如果是,请求出此定值;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划在新农村改造过程中,拟筹资金2000元,计划在一块上、下底分别为10米、20米的梯形空地上种植花草(如图所示,![]() ),村委会想在
),村委会想在![]() 地带与
地带与![]() 地带种植单价为10元的太阳花,当
地带种植单价为10元的太阳花,当![]() 地带种满花后,已经花了500元,请你计算一下,若继续在
地带种满花后,已经花了500元,请你计算一下,若继续在![]() 地带种植同样的太阳花,资金是否够用?并说明理由.
地带种植同样的太阳花,资金是否够用?并说明理由.
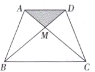
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为_____.
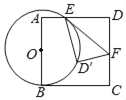
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动。如果P、Q分别从A、B同时出发,设运动时间为t.
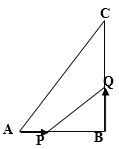
求:(1)当t为何值时,△PBQ的面积等于8cm2?
(2)当t为何值时,△PBQ与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
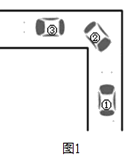
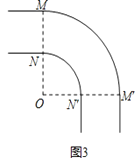
【题目】车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)试说明长8m,宽3m的消防车不能通过该直角转弯;
(2)为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=y1y2,其中y1=![]() +1,y2=
+1,y2=![]() x﹣1,请对该函数及其图象进行如下探究:
x﹣1,请对该函数及其图象进行如下探究:
解析式探究:根据给定的条件,可以确定出该函数的解析式为:______.
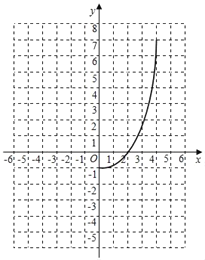
函数图象探究:①根据解析式,完成下表:
x | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | ﹣9 | ﹣ | m | n | ﹣1 | ﹣ | … |
m=______,n=_____.
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出当x≤0时的函数图象;
结合画出的函数图象,解决问题:
①若A(x1,y1)、B(x2,y2)为图象上的两点,满足x1<x2;则y1_____y2(用<、=、>填空).
②写出关于x的方程y1y2=﹣x+3的近似解(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】强哥驾驶小汽车(出租)匀速地从如皋火车站送客到南京绿口机场,全程为280km,设小汽车的行驶时间为t(单位:h),行驶速度为v(单位:km/h),且全程速度限定为不超过120km/h.
(1)求v关于t的函数解析式;
(2)强哥上午8点驾驶小汽车从如皋火车站出发.
①乘客需在当天10点48分至11点30分(含10点48分和11点30分)间到达南京绿口机场,求小汽车行驶速度v的范围;
②强哥能否在当天10点前到达绿口机场?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com