
【题目】在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动。如果P、Q分别从A、B同时出发,设运动时间为t.
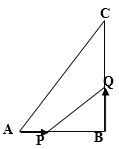
求:(1)当t为何值时,△PBQ的面积等于8cm2?
(2)当t为何值时,△PBQ与△ABC相似?
【答案】(1)如果点P、Q分别从A、B同时出发,经过2或4秒钟,使△PBQ的面积为8cm2.(2)如果点P、Q分别从A、B同时出发,经过3或1.2秒钟,使△PBQ与△ABC相似.
【解析】
(1)根据路程=速度×时间即可用含t的代数式表示线段BP和BQ;若使△PBQ的面积为8cm2,根据三角形的面积公式得出方程,求出即可;
(2)若使△PBQ与△ABC相似,根据两边成比例并且夹角相等的两三角形相似得到第一种情况![]() 和第二种情况
和第二种情况![]() 代入求出即可.
代入求出即可.
(1)∵点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,
∴AP=t,BQ=2t,
∴BP=AB-AP=6-t;
若使△PBQ的面积为8cm2,
∵∠B=90°,
∴![]() BP×BQ=8,
BP×BQ=8,
∴![]() ×(6-t)×2t=8,
×(6-t)×2t=8,
∴t1=2,t2=4,
答:如果点P、Q分别从A、B同时出发,经过2或4秒钟,使△PBQ的面积为8cm2.
(2)若使△PBQ与△ABC相似,
∵∠B=∠B,
第一种情况:当时![]() ,△PBQ与△ABC相似,
,△PBQ与△ABC相似,
即![]() ,
,
解得:t=3,
第二种情况:当![]() 时,△PBQ与△ABC相似,
时,△PBQ与△ABC相似,
即![]() ,
,
解得:t=1.2.
答:如果点P、Q分别从A、B同时出发,经过3或1.2秒钟,使△PBQ与△ABC相似.


科目:初中数学 来源: 题型:
【题目】(9分)某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
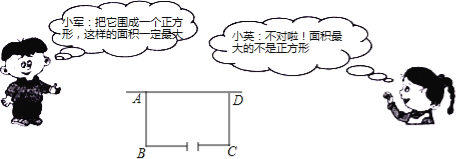
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.
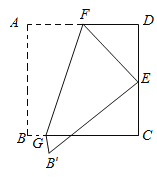
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A、B两点,其中点A的坐标为(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E。现有下列结论:①b2-4ac<0;②b>0;③5a+b>0;④BD+CE=4.其中结论正确的个数为( )
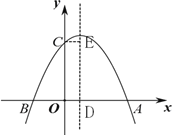
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=ax2+bx+a-5(a、b为常数,a≠0),且2a+b=3.
(1)若该二次函数的图象经过点(-1,4),求该二次函数的解析式.
(2)无论a取何常数,这个二次函数的图象始终经过一个定点,求出这个定点坐标.
(3)已知点P(x0,m)和Q(1,n)都在二次函数的图象上,若x0<1,且m>n,求x0的取值范围(用含a的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c=0;④当y>0时,x的取值范围是﹣1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的是_____(只需填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com