
【题目】如图,在平行四边形纸片![]() 中,
中,![]() ,将纸片沿对角线
,将纸片沿对角线![]() 对折,
对折,![]() 边与
边与![]() 边交于点
边交于点![]() ,此时,
,此时,![]() 恰为等边三角形,则重叠面积为( )
恰为等边三角形,则重叠面积为( )
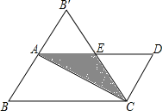
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由△CDE为等边三角形,可知DE=DC=EC,∠D=60°,根据折叠的性质,可知∠BCA=∠ECA,又AD∥BC,可知AE=EC,可知∠DAC=30°,故∠ACD=90°,由BC=AD=4![]() ,则CD=2
,则CD=2![]() ,AC=6,故S△ACE=
,AC=6,故S△ACE=![]() S△ACD=
S△ACD=![]() ×ACCD.
×ACCD.
∵△CDE为等边三角形,
∴DE=DC=EC,∠D=60°,
根据折叠的性质,∠BCA=∠ECA,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAC=∠BCA,
∴∠EAC=∠ECA,
∴EA=EC,
∴∠DAC=30°,
∴∠ACD=90°,
∴CD=![]() AD=2
AD=2![]() ,AC=6,
,AC=6,
∴S△ACE=![]() S△ACD=
S△ACD=![]() ×ACCD=
×ACCD=![]() ×6×2
×6×2![]() =3
=3![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,是一个被等分成8个扇形的转盘.请在扇形内写上“红、黑”表示涂上相应的颜色,未写表示白色,使得自由转动停止后,指针落在红色区域的概率等于落在黑色区域的概率,且小于落在白色区域的概率.填出两种,再指出“红、黑,白”分别是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动。如果P、Q分别从A、B同时出发,设运动时间为t.
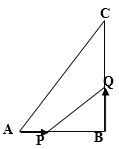
求:(1)当t为何值时,△PBQ的面积等于8cm2?
(2)当t为何值时,△PBQ与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一不透明口袋中装有大小形状完全相同的2个黑球和2个白球,先从口袋中模出一个球,不放回,再从口袋中摸出另一个球,则摸出的两个球颜色不相同的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=y1y2,其中y1=![]() +1,y2=
+1,y2=![]() x﹣1,请对该函数及其图象进行如下探究:
x﹣1,请对该函数及其图象进行如下探究:
解析式探究:根据给定的条件,可以确定出该函数的解析式为:______.
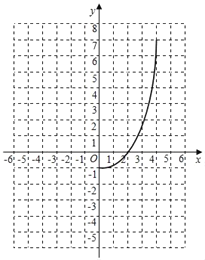
函数图象探究:①根据解析式,完成下表:
x | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | ﹣9 | ﹣ | m | n | ﹣1 | ﹣ | … |
m=______,n=_____.
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出当x≤0时的函数图象;
结合画出的函数图象,解决问题:
①若A(x1,y1)、B(x2,y2)为图象上的两点,满足x1<x2;则y1_____y2(用<、=、>填空).
②写出关于x的方程y1y2=﹣x+3的近似解(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的一个数学兴趣小组在本校学生中开展主题为“买房知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,分别记作![]() 、
、![]() 、
、![]() 、
、![]() ;并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
;并根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
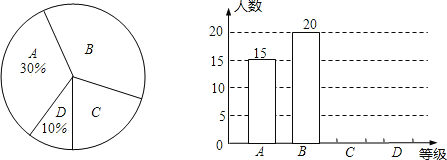
(1)求本次被调查的学生共有多少人?并将条形统计图和扇形统计图补充完整;
(2)在“比较了解”的调查结果里,初三年级学生共有5人,其中2男3女,在这5人中,打算随机选出2位进行采访,请你用列表法或树状图的方法求出所选两位同学至少有一位是男同学的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
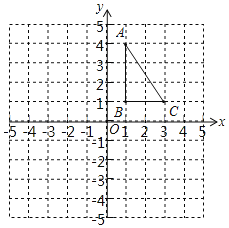
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC绕O点顺时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求点C划过的路径长度(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在东西方向的海岸线![]() 两艘船,均收到已触礁搁浅的船
两艘船,均收到已触礁搁浅的船![]() 的求救信号,已知船
的求救信号,已知船![]() 在船
在船![]() 的北偏东58°方向,船
的北偏东58°方向,船![]() 在船
在船![]() 的北偏西35°方向,且
的北偏西35°方向,且![]() 的距离为30海里.观察图形并回答问题:(参考数据:
的距离为30海里.观察图形并回答问题:(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
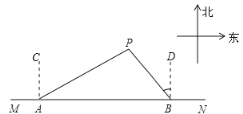
(1)求船![]() 到海岸线
到海岸线![]() 的距离(精确到0.1海里);
的距离(精确到0.1海里);
(2)若船![]() 、船
、船![]() 分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船
分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船![]() 处.
处.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com