
【题目】在一不透明口袋中装有大小形状完全相同的2个黑球和2个白球,先从口袋中模出一个球,不放回,再从口袋中摸出另一个球,则摸出的两个球颜色不相同的概率为______.
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质:
的图象与性质:
小宏根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小宏的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … | ﹣ | ﹣ | 0 | m |
| ﹣ | ﹣ | 0 |
| n | … |
求m,n的值;
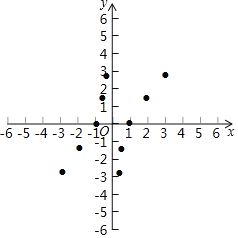
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的性质(两条即可):
①
② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A、B两点,其中点A的坐标为(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E。现有下列结论:①b2-4ac<0;②b>0;③5a+b>0;④BD+CE=4.其中结论正确的个数为( )
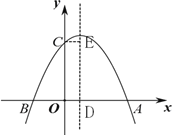
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c=0;④当y>0时,x的取值范围是﹣1≤x<3;⑤当x<0时,y随x增大而增大,其中结论正确的是_____(只需填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=![]() 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】炎热的夏天来临之际.为了调查我校学生消防安全知识水平,学校组织了一次全校的消防安全知识培训,培训完后进行测试,在全校2400名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
男生15名学生测试成绩统计如下:
68,72,89,85,82,85,74,92,80,85,76,85,69,78,80
女生15名学生测试成绩统计如下:(满分100分)
82,88,83,76,73,78,67,81,82,80,80,86,82,80,82
按如下分数段整理、描述这两组样本数据:
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
男生 | 2 | 2 | 4 | 5 | 1 | 1 |
女生 | 1 | 1 | 5 | 6 | 2 | 0 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 80 | x | 80 | 45.9 |
女生 | 80 | 82 | y | 24.3 |
在表中:x=_____;y=_____.
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中消防安全知识合格的学生有______人.
(3)通过数据分析得到的结论是女生掌握消防安全相关知识的整体水平比男生好,请从两个方面说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解决问题:
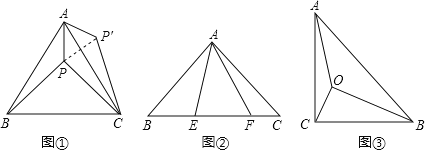
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=__________;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家的阳台上放置了一个晒衣架如图①.图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面.经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm.垂挂在衣架上的连衣裙总长度小于________cm时,连衣裙才不会拖落到地面上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com